题目内容
15.设数列{an}的前n项和为Sn,对任意正整数n,3an-2Sn=2.(I)求数列{an}的通项公式;
(Ⅱ)求证:Sn+2Sn<${S}_{n+1}^{2}$.
分析 (I)对任意正整数n,3an-2Sn=2,可得3a1-2a1=2,解得a1.当n≥2时,3an-1-2Sn-1=2,可得an=3an-1,利用等比数列的通项公式即可得出.(2)证明:由(I)可得:Sn=3n-1.作差代入Sn+2Sn-${S}_{n+1}^{2}$<0,即可证明.<${S}_{n+1}^{2}$.
解答 (I)解:∵对任意正整数n,3an-2Sn=2,∴3a1-2a1=2,解得a1=2.
当n≥2时,3an-1-2Sn-1=2,可得3an-3an-1-2an=0,化为an=3an-1,
∴数列{an}是等比数列,公比为3,首项为2.
∴an=2×3n-1.
(2)证明:由(I)可得:Sn=$\frac{2({3}^{n}-1)}{3-1}$=3n-1.
∴Sn+2Sn-${S}_{n+1}^{2}$=(3n+2-1)(3n-1)-(3n+1-1)2=-4×3n<0,
∴Sn+2Sn<${S}_{n+1}^{2}$.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)的解析式可能为( )
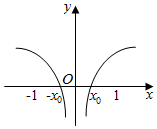

| A. | $\frac{{e}^{x}}{x}$ | B. | x2•lnx | C. | $\frac{{e}^{|x|}}{x}$ | D. | x•lnx2 |
4.某医院准备从6名骨科大夫中选派3名去农村三处医疗所做培训,要求甲、乙两位骨科组长至少有一人参加,那么不同的选派种数为( )
| A. | 96 | B. | 72 | C. | 60 | D. | 30 |