题目内容
2.已知函数f(x)=$\frac{x-2}{x-1}$与g(x)═mx+1-m的图象相交于点A,B两点,若动点P满足|$\overrightarrow{PA}$+$\overrightarrow{PB}$|=2,则P的轨迹方程是(x-1)2+(y-1)2=4.分析 联立直线方程和双曲线方程,求得A,B的坐标,写出向量的坐标,求出两向量的坐标和,由向量的模等于2化简整理得到P的轨迹方程.
解答 解:联立函数f(x)=$\frac{x-2}{x-1}$与g(x)═mx+1-m得x=1±$\sqrt{-\frac{1}{m}}$.
当x=1-$\sqrt{-\frac{1}{m}}$时,y=1-m$\sqrt{-\frac{1}{m}}$,
当x=1+$\sqrt{-\frac{1}{m}}$时,y=1+m$\sqrt{-\frac{1}{m}}$,
设动点P(x,y),
则$\overrightarrow{PA}$=(1-$\sqrt{-\frac{1}{m}}$-x,1-m$\sqrt{-\frac{1}{m}}$-y),
$\overrightarrow{PB}$=(1+$\sqrt{-\frac{1}{m}}$-x,1+m$\sqrt{-\frac{1}{m}}$-y),
则$\overrightarrow{PA}$+$\overrightarrow{PB}$=(2-2x,2-2y),
由|$\overrightarrow{PA}$+$\overrightarrow{PB}$|=2,得(2-2x)2+(2-2y)2=4,即(x-1)2+(y-1)2=4,
∴P的轨迹方程是(x-1)2+(y-1)2=4,
故答案为(x-1)2+(y-1)2=4.
点评 本题考查了轨迹方程的求法,考查了平面向量的坐标运算,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.随机变量X的概率分布列如下表如示,且$P(X=n)=\left\{\begin{array}{l}\frac{7}{10},n=1\\ \frac{1}{n(n+1)},n≥2且n∈z\end{array}\right.$,
(Ⅰ)由分布列的性质试求n的值,并求随机变量X的分布列与数学期望;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不小于3的概率.
| X | X1 | X2 | X3 | … | Xn |
| P | p1 | p2 | p3 | … | pn |
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不小于3的概率.
7.已知函数f(x)=x3+sinx,x∈(-1,1).如果f(1-a)+f(1-a2)<0,则a的取值范围是( )
| A. | $(1,\sqrt{2})$ | B. | (-∞,-2)∪(1,+∞) | C. | (-∞,-1)∪(2,+∞) | D. | $(0,\sqrt{2})$ |
14.下列有关命题的说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 命题“?x∈R,x2+2x-1<0”的否定是“?x∈R,x2+2x-1>0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 若“p或q”为真命题,则p,q至少有一个为真命题 |
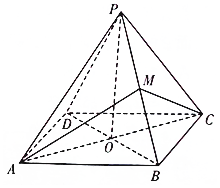 四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.
四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.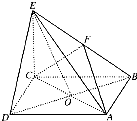 四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.
四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.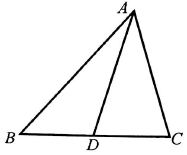 已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.
已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.