题目内容
1．在△ABC中，a，b，c分别是内角A，B，C的对边，若bsinA=3csinB，a=3，$cosB=\frac{2}{3}$，则b=（ ）| A． | 14 | B． | 6 | C． | $\sqrt{14}$ | D． | $\sqrt{6}$ |
分析 bsinA=3csinB，利用正弦定理可得ab=3cb，化简解得c，再利用余弦定理即可得出．
解答 解：在△ABC中，∵bsinA=3csinB，
∴ab=3cb，可得a=3c，
∵a=3，∴c=1．
∴$cosB=\frac{2}{3}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{9+1-{b}^{2}}{2×3×1}$，
解得b=$\sqrt{6}$．
故选：D．
点评 本题考查了正弦定理余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
11．正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$，在正方体表面上与点A距离是2的点形成一条封闭的曲线，这条曲线的长度是（ ）
| A． | π | B． | $\frac{3}{2}π$ | C． | 3π | D． | $\frac{5}{2}π$ |
12．设x∈（0，π），若$\frac{1}{sinx}+\frac{1}{cosx}=2\sqrt{2}$，则$sin（2x+\frac{π}{3}）$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
16．
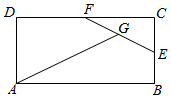如图，在矩形ABCD中，AB=2AD，E，F分别为BC，CD的中点，G为EF中点，
则$\overrightarrow{AG}$=（ ）
如图，在矩形ABCD中，AB=2AD，E，F分别为BC，CD的中点，G为EF中点，则$\overrightarrow{AG}$=（ ）
| A． | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B． | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C． | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D． | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |