题目内容
7.已知函数$g(x)=\frac{{{4^x}-a}}{2^x}$是奇函数,f(x)=lg(10x+1)+bx是偶函数.(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2-2t)+g(2t2-k)>0恒成立,求实数k的取值范围.
(3)设$h(x)=f(x)+\frac{1}{2}x$,若存在x∈(-∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
分析 (1)由条件利用函数的奇偶性的性质求得a、b的值,可得a+b的值.
(2)由条件利用函数的单调性求得3t2-2t>k,t∈[0,+∞)恒成立,求得3t2-2t的最小值,可得k的范围.
(3)由题意可得存在x∈(-∞,1],使不等式g(x)>lg(10a+10)成立,求得g(x)的最大值,可得a的范围.
解答 解:(1)由g(0)=0得a=1,则$g(x)=\frac{{{4^x}-1}}{2^x}$,经检验g(x)是奇函数.
由f(-1)=f(1)得$b=-\frac{1}{2}$,则$f(x)=lg({10^x}+1)-\frac{1}{2}x$,经检验f(x)是偶函数,
∴$a+b=\frac{1}{2}$.
(2)∵$g(x)=\frac{{{4^x}-1}}{2^x}={2^x}-\frac{1}{2^x}$,且g(x)在(-∞,+∞)单调递增,且g(x)为奇函数.
∴由g(t2-2t)+g(2t2-k)>0恒成立,得g(t2-2t)>-g(2t2-k)=g(-2t2+k),
∴t2-2t>-2t2+k,t∈[0,+∞)恒成立,
即3t2-2t>k,t∈[0,+∞)恒成立,
令F(x)=3t2-2t,在[0,+∞)上F(x)的最小值为$F(\frac{1}{3})=-\frac{1}{3}$,∴$k<-\frac{1}{3}$.
(3)h(x)=lg(10x+1),h(lg(10a+9))=lg[10lg(10a+9)+1]=lg(10a+10),
则由已知得,存在x∈(-∞,1],使不等式g(x)>lg(10a+10)成立,
而g(x)在(-∞,1]单增,∴${g_{max}}(x)=g(1)=\frac{3}{2}$,
∴$lg(10a+10)<\frac{3}{2}=lg{10^{\frac{3}{2}}}={lg^{10\sqrt{10}}}$,∴$10a+10<10\sqrt{10}$.
又$a<\sqrt{10}-1$,
∵$\left\{\begin{array}{l}10a+9>0\\ 10a+10>0\end{array}\right.$,∴$a>-\frac{9}{10}$,
∴$-\frac{9}{10}<a<\sqrt{10}-1$.
点评 本题主要考查函数的奇偶性的性质,函数的单调性,函数的恒成立与能成立问题,属于中档题.

| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
| A. | (-$\frac{1}{7}$,$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{7}$)∪($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{7}$,$\frac{1}{2}$) | D. | (-$\frac{1}{7}$,$\frac{1}{2}$] |
| A. | -3.3 m/s | B. | 3.3 m/s | C. | -11.6 m/s | D. | 11.6 m/s |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
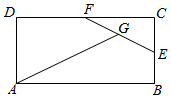 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |
| A. | [-2,-1] | B. | [-1,2) | C. | [-2,1] | D. | [1,2) |