题目内容
6.已知f(x)=m•2x+x2+nx,若{x|f(x)=0}={x|f(f(x))=0}≠∅,则m+n的取值范围为( )| A. | (0,4) | B. | [0,4) | C. | (0,5] | D. | [0,5] |
分析 由{x|f(x)=0}={x|f(f(x))=0}可得f(0)=0,从而求得m=0;从而化简f(f(x))=(x2+nx)(x2+nx+n)=0,从而讨论求得.
解答 解:设x1∈{x|f(x)=0}={x|f(f(x))=0},
∴f(x1)=f(f(x1))=0,
∴f(0)=0,
即f(0)=m=0,
故m=0;
故f(x)=x2+nx,
f(f(x))=(x2+nx)(x2+nx+n)=0,
当n=0时,成立;
当n≠0时,0,-n不是x2+nx+n=0的根,
故△=n2-4n<0,
故0<n<4;
综上所述,0≤n+m<4;
故选B.
点评 本题考查了函数与集合的关系应用及分类讨论的思想应用,同时考查了方程的根的判断,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
1.下列命题中,正确的是( )
| A. | 复数的模总是正实数 | |
| B. | 复数集与复平面内所有向量组成的集合一一对应 | |
| C. | 如果与复数z对应的点在第一象限,则与该复数对应的向量的终点也一定会在第一象限 | |
| D. | 相等的向量对应着相等的复数 |
2.已知命题p:?x∈N*,($\frac{1}{2}$)x≥($\frac{1}{3}$)x,命题q:?x∈N*,2x+21-x=2$\sqrt{2}$,则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
19.已知数列{an}是等比数列,且a5-a3=${∫}_{-1}^{1}$(x2+sinx)dx,则a32-2a2a6+a3a7=( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | 1 | D. | $\frac{8}{3}$ |
11.正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,在正方体表面上与点A距离是2的点形成一条封闭的曲线,这条曲线的长度是( )
| A. | π | B. | $\frac{3}{2}π$ | C. | 3π | D. | $\frac{5}{2}π$ |
18.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{\frac{x}{2}}-1,0<x≤4}\\{|x-7|,x>4}\end{array}\right.$,若方程f(x)=kx+1有三个不同的实数根,则实数k的取值范围是( )
| A. | (-$\frac{1}{7}$,$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{7}$)∪($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{7}$,$\frac{1}{2}$) | D. | (-$\frac{1}{7}$,$\frac{1}{2}$] |
15.在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A. | -3.3 m/s | B. | 3.3 m/s | C. | -11.6 m/s | D. | 11.6 m/s |
16.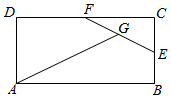 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
则$\overrightarrow{AG}$=( )
 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,则$\overrightarrow{AG}$=( )
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |