题目内容
已知两定点A(1,0),B(-1,0),动点P在y轴上的射影为Q,
•
+
=0
(1)求动点P的轨迹E的方程;
(2)直线l交y轴于点C(0,m),交轨迹E于M,N两点,且满足
=3
,求实数m的取值范围.
| PA |
| PB |
| PQ |
(1)求动点P的轨迹E的方程;
(2)直线l交y轴于点C(0,m),交轨迹E于M,N两点,且满足
| MC |
| CN |
考点:平面向量数量积的运算,轨迹方程
专题:平面向量及应用,向量与圆锥曲线
分析:(1)首先根据向量的坐标求出向量的数量积,和向量的模,根据条件求出轨迹的方程.
(2)进一步利用第一步的结论,与直线建立方程组,然后根据
得到:(2+k2)x2+2kmx+m2-1=0,利用判别式建立m和k的关系式,进一步利用条件得到横坐标的关系,然后利用根和系数的关系求出参数的取值范围.
(2)进一步利用第一步的结论,与直线建立方程组,然后根据
|
解答:
解:(1)设P(x,y),则:
P在y轴上的射影为Q,Q(0,y)
则:
=(1-x,-y),
=(-1-x,-y),
=(-x,0)
所以:
2=x2
由于:
•
+
2=0
所以:x2+y2-1+x2=0
即:2x2+y2=1
所以:动点P的轨迹E的方程为:2x2+y2=1
(2)直线l交y轴于点C(0,m),则:设直线的方程为:y=kx+m,
与轨迹E的坐标M(x1,y1),N(x2,y2)
则:联立的方程组为:
整理得:(2+k2)x2+2kmx+m2-1=0
所以△=4k2m2-4(2+k2)(m2-1)>0
整理得:2+k2>2m2
所以:x1+x2=
,x1x2=
又:
=3
则:-x1=3x2
所以:k2(4m2-1)=2-2m2
整理得:2+
>2m2
化简为:
<m2<1
解得:-1<m<-
或
<m<1.
所以:实数m的取值范围为:-1<m<-
或
<m<1
P在y轴上的射影为Q,Q(0,y)
则:
| PA |
| PB |
| PQ |
所以:
| PQ |
由于:
| PA |
| PB |
| PQ |
所以:x2+y2-1+x2=0
即:2x2+y2=1
所以:动点P的轨迹E的方程为:2x2+y2=1
(2)直线l交y轴于点C(0,m),则:设直线的方程为:y=kx+m,
与轨迹E的坐标M(x1,y1),N(x2,y2)
则:联立的方程组为:
|
整理得:(2+k2)x2+2kmx+m2-1=0
所以△=4k2m2-4(2+k2)(m2-1)>0
整理得:2+k2>2m2
所以:x1+x2=
| -2km |
| 2+k2 |
| m2-1 |
| 2+k2 |
又:
| MC |
| CN |
则:-x1=3x2
所以:k2(4m2-1)=2-2m2
整理得:2+
| 2-2m2 |
| 4m2-1 |
化简为:
| 1 |
| 4 |
解得:-1<m<-
| 1 |
| 2 |
| 1 |
| 2 |
所以:实数m的取值范围为:-1<m<-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的知识要点:向量的坐标运算,向量的数量积,轨迹方程的求法,根与系数的关系,利用方程组求参数的取值范围.属于难题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
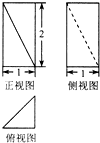
如图是某几何体的三视图,则该几何体的体积等于( )

A、
| ||
B、
| ||
| C、1 | ||
D、
|
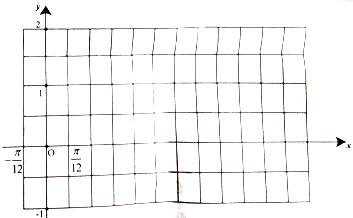 设
设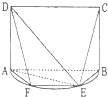 如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.
如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.