题目内容
16.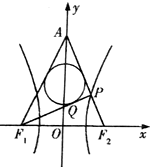 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 由|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,根据切线长定理,可得|PF1|-|PF2|=2,结合|F1F2|=6,即a=1,c=3,由离心率公式,可得出结论.
解答 解:由题意,∵|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,
如图,根据切线长定理可得AM=AN,F1M=F1Q,PN=PQ,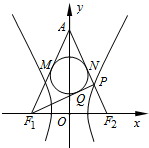
∵|AF1|=|AF2|,
∴AM+F1M=AN+PN+NF2,
∴F1M=PN+NF2=PQ+PF2
∴|PF1|-|PF2|=F1Q+PQ-PF2=F1M+PQ-PF2=PQ+PF2+PQ-PF2=2PQ=2,
又|F1F2|=6,可得c=3,a=1.
∴双曲线的离心率是e=$\frac{c}{a}$=3.
故选:A.
点评 本题考查双曲线的离心率,考查三角形内切圆的性质,考查切线长定理,学生的计算能力,属于中档题.

练习册系列答案
相关题目
4.已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a,b>0)的左、右焦点分别为F1,F2,过F2作双曲线C的一条渐近线的垂线,垂足为H,若F2H的中点M在双曲线C上,则双曲线C的渐近线方程为( )
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2$\sqrt{2}$x |
8.若I,∅分别表示全集与空集,且(∁IP)∪M?P,则集合P,M必须满足( )
| A. | ∅?P?M | B. | M?P?I | C. | M=∅ | D. | P=I且M≠P |