题目内容
3.已知A=N*,B={$\frac{1}{3}$,$\frac{3}{5}$,$\frac{5}{7}$,…},映射f:x→y=$\frac{2x-1}{2x+1}$(x∈A,y∈B),则在f的作用下,象$\frac{15}{17}$的原象( )| A. | $\frac{29}{35}$ | B. | $\frac{15}{17}$ | C. | 8 | D. | 9 |
分析 直接把y=$\frac{15}{17}$代入y=$\frac{2x-1}{2x+1}$求得x值得答案.
解答 解:由映射f:x→y=$\frac{2x-1}{2x+1}$(x∈A,y∈B),
可得$\frac{2x-1}{2x+1}$=$\frac{15}{17}$,解得x=8.
∴象$\frac{15}{17}$的原象是8.
故选:C.
点评 本题考查映射的概念,对概念的理解是解答该题的关键,是基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.如图,线段AB与CD互相平分,则$\overrightarrow{BD}$可以表示为( )
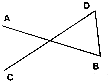

| A. | $\overrightarrow{AB}$-$\overrightarrow{CD}$ | B. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{CD}$ | C. | $\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{CD}$) | D. | -($\overrightarrow{AB}$-$\overrightarrow{CD}$) |
8.若I,∅分别表示全集与空集,且(∁IP)∪M?P,则集合P,M必须满足( )
| A. | ∅?P?M | B. | M?P?I | C. | M=∅ | D. | P=I且M≠P |
13.已知集合M={x|y=$\frac{1}{\sqrt{4-2x}}$+1},集合N={y|y=-x2+4x-2},则集合M与集合N的关系为( )
| A. | M?N | B. | M?N | C. | M=N | D. | M?N |
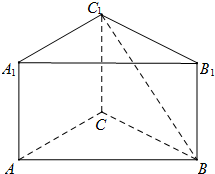 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4