题目内容
2．
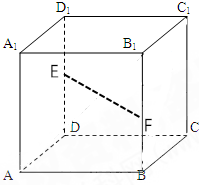如图，在正方体ABCD-A1B1C1D1中，点E是DD1的中点，点F是BB1的中点．求证：EF∥平面ABCD．
分析 连结BD，则根据正方体的结构特征可知四边形BDEF为平行四边形，得出EF∥BD，故而EF∥平面ABCD．
解答 
证明：连结BD，
∵正方体ABCD-A1B1C1D1，
∴BB1∥DD1，BB1=DD1，
∵点E是DD1的中点，点F是BB1的中点，
∴BF∥DE，BF=DE，
∴四边形BDEF是平行四边形，
∴EF∥BD，又EF?平面ABCD，BD?平面ABCD，
∴EF∥平面ABCD．
点评 本题考查了线面平行的判定定理，属于基础题．
练习册系列答案
相关题目
12．函数f（x）=（$\frac{1}{2}$）${\;}^{2x-{x}^{2}}$的值域为（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | [1，+∞） | C． | （0，+∞） | D． | R |
13．如图，线段AB与CD互相平分，则$\overrightarrow{BD}$可以表示为（ ）
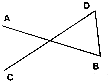
| A． | $\overrightarrow{AB}$-$\overrightarrow{CD}$ | B． | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{CD}$ | C． | $\frac{1}{2}$（$\overrightarrow{AB}$-$\overrightarrow{CD}$） | D． | -（$\overrightarrow{AB}$-$\overrightarrow{CD}$） |
10．若x＞0，则-4x-$\frac{1}{x}$（ ）
| A． | 有最大值 | B． | 有最小值 | ||
| C． | 既无最大值又无最小值 | D． | 不确定 |
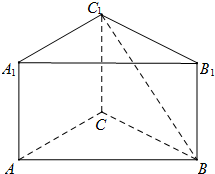如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=3，BC=CC1=4