题目内容
17.已知数列{an}满足an=$\left\{\begin{array}{l}{(1-2a)n+1,n>3}\\{{a}^{n-2},1≤n≤3}\end{array}\right.$(n∈N*),若对于任意的n∈N*都有an>an+1,则实数a的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{5}{9}$) | C. | ($\frac{1}{2}$,$\frac{5}{9}$) | D. | ($\frac{5}{9}$,1) |
分析 由题意结合分段函数的单调性列关于a的不等式组,则答案可求.
解答 解:由an=$\left\{\begin{array}{l}{(1-2a)n+1,n>3}\\{{a}^{n-2},1≤n≤3}\end{array}\right.$(n∈N*),且对于任意的n∈N*都有an>an+1,
则$\left\{\begin{array}{l}{1-2a<0}\\{0<a<1}\\{a>4(1-2a)+1}\end{array}\right.$,解得:$\frac{1}{2}<a<\frac{5}{9}$.
∴实数a的取值范围是($\frac{1}{2}$,$\frac{5}{9}$).
故选:C.
点评 本题考查数列递推式,考查了数列的函数特性,考查了分段函数单调性,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.若双曲线2kx2-ky2=1的一个焦点的坐标为(0,4),则k的值为( )
| A. | $\frac{3}{32}$ | B. | $\frac{16}{3}$ | C. | -$\frac{3}{32}$ | D. | -$\frac{16}{3}$ |
12.有5本不同的书,其中语文书2本,数学书2本,物理书1本,若从中任抽一本,抽到的书是数学书的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
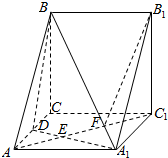 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.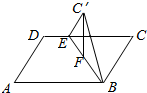 已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.