题目内容
12．三棱锥A-BCD中，AB=AC=AD=2，∠BAD=90°，∠BAC=60°，则$\overrightarrow{AB}$•$\overrightarrow{CD}$等于（ ）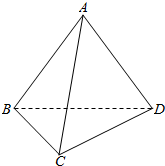
| A． | -2 | B． | 2 | C． | -2$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
分析 用$\overrightarrow{AD}，\overrightarrow{AC}$表示出$\overrightarrow{CD}$，再计算数量积．
解答 解：∵$\overrightarrow{CD}=\overrightarrow{AD}-\overrightarrow{AC}$，∴$\overrightarrow{AB}$•$\overrightarrow{CD}$=$\overrightarrow{AB}$•（$\overrightarrow{AD}-\overrightarrow{AC}$）=$\overrightarrow{AB}•\overrightarrow{AD}$-$\overrightarrow{AB}•\overrightarrow{AC}$=2×2×cos90°-2×2×cos60°=-2．
故选：A．
点评 本题考查了平面向量的数量积运算，向量线性运算的三角形法则，属于基础题．
练习册系列答案
相关题目
3．当x＞0时，x2+mx+1≥0恒成立，且关于t的不等式t2+2t+m≤0有解，则实数m的取值范围是（ ）
| A． | [1，+∞） | B． | [-2，1] | C． | （-∞，-2]∪[1，+∞） | D． | （-∞，-2] |
如图所示，在四棱锥A-BCDE中，AE⊥平面BCDE．△BCE是正三角形，BD和CE的交点恰好平分CE，又AE=BE=2，∠CDE=120°，AG=$\frac{\sqrt{2}}{2}$．