题目内容
7.若角$\frac{α}{2}$与-$\frac{π}{8}$的终边重合,则α=4k$π-\frac{π}{4}$,k∈Z.分析 利用终边相同的角的表示方法,列出方程,求出α的值.
解答 解:因为角$\frac{α}{2}$与-$\frac{π}{8}$的终边重合,
所以$\frac{α}{2}$=2k$π-\frac{π}{8}$,k∈Z
解得α=4k$π-\frac{π}{4}$,k∈Z
故答案为:4k$π-\frac{π}{4}$,k∈Z.
点评 本题考查终边相同的角的表示方法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.设某几何体的三视图如图(长度单位为cm),则该几何体的最长的棱为( )cm
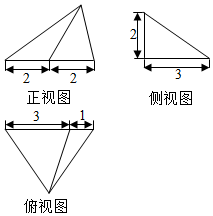

| A. | 4cm | B. | $\sqrt{13}$cm | C. | $\sqrt{14}$cm | D. | $\sqrt{15}$cm |
12.三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则$\overrightarrow{AB}$•$\overrightarrow{CD}$等于( )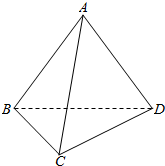

| A. | -2 | B. | 2 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |