题目内容
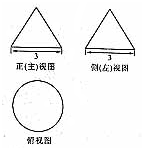 已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )
已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )A、
| ||||
| B、9π | ||||
C、
| ||||
| D、12π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据三视图判断底面半径为r=
,l=3的圆锥,求出高得出此几何体的体积为
×π×(
)2×
=
.
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
9
| ||
| 8 |
解答:
解:∵ 根据三视图可判断:底面半径为r=
根据三视图可判断:底面半径为r=
,l=3的圆锥,
∴高h=
,
∵故选:C
 根据三视图可判断:底面半径为r=
根据三视图可判断:底面半径为r=| 3 |
| 2 |
∴高h=
3
| ||
| 2 |
∵故选:C
点评:本题考查了学生的空间想象力,根据三视图确定空间几何体,属于基础题.

练习册系列答案
相关题目
如图是不锈钢保温饭盒的三视图,根据图中数据(单位:cm),则该饭盒的表面积为( )

| A、1100πcm2 |
| B、900πcm2 |
| C、800πcm2 |
| D、600πcm2 |
已知某个几何体的三视图如图,则该几何体的体积为( )


| A、π+4 | ||
B、
| ||
C、
| ||
D、π+
|
已知实数x,y满足
,则点(x,y)在函数f(x)=
的图象与坐标轴所围成的封闭图形的内部的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数z=
,则z为( )
| 1-i |
| 1+i |
| A、i | B、-i | C、2i | D、1+i |
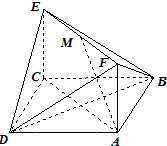 如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=