题目内容
若实数x，y满足xy=4，则x2+4y2的最小值为 ．
考点：基本不等式
专题：不等式的解法及应用
分析：由已知可得y=
，代入要求的式子，由基本不等式可得．
| 4 |
| x |
解答：
解：∵xy=4，
∴y=
∴x2+4y2=x2+
≥2
=16，当且仅当x2=
，即x=±2
时取等号，
故答案为：16
∴y=
| 4 |
| x |
∴x2+4y2=x2+
| 64 |
| x2 |
x2•
|
| 64 |
| x2 |
| 2 |
故答案为：16
点评：本题考查基本不等式，属基础题．
练习册系列答案
小学教材完全解读系列答案
相关题目
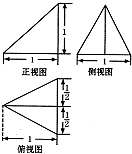
已知某几何体的三视图，根据图中标出的尺寸，可得这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
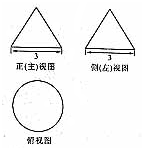已知一个几何体的正（主）视图及侧（左）视图均是边长为3的正三角形，俯视图是直径为3的圆，则此几何体的体积为（ ）A、
| ||||
| B、9π | ||||
C、
| ||||
| D、12π |
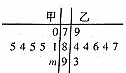如图为甲，乙两名学生7次考试成绩的茎叶图（其中m为数字0～9中的一个），去掉一个最高分和一个最低分后，甲、乙考试成绩的平均数分别为a和b，则一定有（ ）| A、a＞b |
| B、a＜b |
| C、a=b |
| D、a，b的大小与m的值有关 |
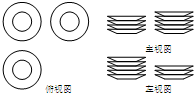一张桌子上摆放有若干个大小、形状完全相同的碟子，现从三个方向看，三种视图如下所示，则这张桌子上碟子的个数为（ ）| A、11 | B、12 | C、13 | D、14 |