题目内容
下列命题中:
①分别和两条异面直线均相交的两条直线一定是异面直线
②一个平面内任意一点到另一个平面的距离均相等,那么这平面平行
③三棱锥的四个面可以都是直角三角形
④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交
⑤已知平面α,直线a和直线b,且a∩α=a,b⊥a,则b⊥α
其中正确命题的序号是 (请填上所有你认为正确命题的序号)
①分别和两条异面直线均相交的两条直线一定是异面直线
②一个平面内任意一点到另一个平面的距离均相等,那么这平面平行
③三棱锥的四个面可以都是直角三角形
④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交
⑤已知平面α,直线a和直线b,且a∩α=a,b⊥a,则b⊥α
其中正确命题的序号是
考点:命题的真假判断与应用
专题:空间角,简易逻辑
分析:举例说明①错误;由两面平行的定义说明②正确;举例说明③④正确;由反证法说明⑤错误.
解答:
解:对于①,分别和两条异面直线均相交的两条直线一定是异面直线错误,若两条直线交原异面直线中的一条于一点,交另一条于两点,则两直线相交;
对于②,一个平面内任意一点到另一个平面的距离均相等,则两平面无交点,两平面平行,命题②正确;
对于③,三棱锥的四个面可以都是直角三角形正确,如三条侧棱两两垂直,底面是直角三角形,③正确;
对于④,过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交错误,如点在经过两异面直线中的一条,且与另一条平行的面内;
对于⑤,已知平面α,直线a和直线b,且a∩α=A,b⊥a,则b⊥α错误,原因是,若b⊥α,又b⊥a,可得a∥α或a?α,与a∩α=A矛盾.
∴正确的命题是②③.
故答案为:②③.
对于②,一个平面内任意一点到另一个平面的距离均相等,则两平面无交点,两平面平行,命题②正确;
对于③,三棱锥的四个面可以都是直角三角形正确,如三条侧棱两两垂直,底面是直角三角形,③正确;
对于④,过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交错误,如点在经过两异面直线中的一条,且与另一条平行的面内;
对于⑤,已知平面α,直线a和直线b,且a∩α=A,b⊥a,则b⊥α错误,原因是,若b⊥α,又b⊥a,可得a∥α或a?α,与a∩α=A矛盾.
∴正确的命题是②③.
故答案为:②③.
点评:本题考查了命题的真假判断与应用,考查了空间中的点、线、面的位置关系,考查了学生的空间想象能力和思维能力,是基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
已知某几何体的三视图,根据图中标出的尺寸,可得这个几何体的体积是( )
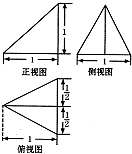

A、
| ||
B、
| ||
C、
| ||
D、
|
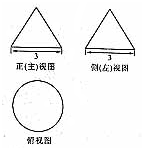 已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )
已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )A、
| ||||
| B、9π | ||||
C、
| ||||
| D、12π |