题目内容
13．设函数f（x）=（x-a）（x-b）（x-c）（a、b、c是互不相等的实数），则$\frac{a}{{f}^{'}（a）}$+$\frac{b}{{f}^{'}（b）}$+$\frac{c}{{f}^{'}（c）}$=0．分析 分别求出f′（a）=（a-b）（a-c），f′（b）=（b-a）（b-c），f′（c）=（c-a）（c-b）．由此能求出$\frac{a}{{f}^{'}（a）}$+$\frac{b}{{f}^{'}（b）}$+$\frac{c}{{f}^{'}（c）}$．
解答 解：∵函数f（x）=（x-a）（x-b）（x-c）（a、b、c是互不相等的实数），
∴f（x）=x3-（a+b+c）x2+（ab+bc+ca）x-abc，
∴f′（x）=3x2-2（a+b+c）x+ab+bc+ca．
又f′（a）=（a-b）（a-c），
同理f′（b）=（b-a）（b-c），
f′（c）=（c-a）（c-b）．
∴$\frac{a}{{f}^{'}（a）}$+$\frac{b}{{f}^{'}（b）}$+$\frac{c}{{f}^{'}（c）}$
=$\frac{a}{（a-b）（a-c）}+\frac{b}{（b-a）（b-c）}$+$\frac{c}{（c-a）（c-b）}$
=$\frac{a（b-c）-b（a-c）+c（a-b）}{（a-b）（a-c）（b-c）}$
=0．
故答案为：0．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
3．
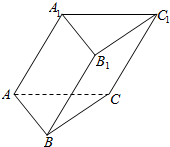如图，在三棱柱ABC-A1B1C1中，各棱长均相等，且∠A1AB=∠A1AC=∠BAC=60°，则AB1与底面ABC所成角的正弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，各棱长均相等，且∠A1AB=∠A1AC=∠BAC=60°，则AB1与底面ABC所成角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |