题目内容
3．抛物线y2=-2px（p＞0）的准线与圆（x-1）2+y2=1相切，则此抛物线上一点P（-3，m）到焦点的距离为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 由抛物线y2=-2px（p＞0）的准线与圆（x-1）2+y2=1相切，解得p=2，利用抛物线的定义，求出抛物线上一点P（-3，m）到焦点的距离．
解答 解：∵抛物线y2=-2px（p＞0）的准线与圆（x-1）2+y2=1相切，
∴$\frac{p}{2}$-1=1，解得p=4．
∴此抛物线上一点P（-3，m）到焦点的距离为2+3=5，
故选：B．
点评 本题考查抛物线的相关几何性质及直线与圆的位置关系等基础知识，考查运算求解能力，考查数形结合思想，注意应用直线与圆相切时圆心到直线的距离等于半径．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．
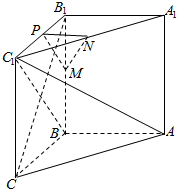如图所示，在直三棱柱ABC-A1B1C1中，∠ABC=90°，BC=CC1，M、N、P分别是BB1、A1C1、B1C1的中点．
（1）求证：CB1⊥平面ABC1；
（2）求证：面MNP∥面ABC1．
如图所示，在直三棱柱ABC-A1B1C1中，∠ABC=90°，BC=CC1，M、N、P分别是BB1、A1C1、B1C1的中点．（1）求证：CB1⊥平面ABC1；
（2）求证：面MNP∥面ABC1．
12．已知函数f（x）=sinωx-$\sqrt{3}$cosωx（ω＞0）的图象的相邻两对称轴间的距离为$\frac{π}{2}$，则当x∈[-$\frac{π}{2}$，0]时，f（x）的最大值和单调增区间分别为（ ）
| A． | 1，[-$\frac{π}{2}$，-$\frac{π}{6}$] | B． | 1，[-$\frac{π}{2}$，-$\frac{π}{12}$] | C． | $\sqrt{3}$，[-$\frac{π}{6}$，0] | D． | $\sqrt{3}$，[-$\frac{π}{12}$，0] |