题目内容
10.若过点P(1,1)可作圆C:x2+y2+mx+my+2=0的两条切线,则实数m的取值范围是( )| A. | (2,+∞) | B. | (-4,+∞) | C. | (-2,+∞) | D. | (-4,-2)∪(2,+∞) |
分析 过点P可作圆x2+y2+mx+my+2=0的两条切线,即P在圆外,把已知圆的方程化为标准方程后,找出圆心坐标和半径r,列出关于m的不等式,同时考虑$\frac{{m}^{2}}{2}$-2大于0,两不等式求出公共解集即可得到m的取值范围.
解答 解:把圆的方程化为标准方程得:(x+$\frac{m}{2}$)2+(y+$\frac{m}{2}$)2=$\frac{{m}^{2}}{2}$-2,
所以圆心坐标为(-$\frac{m}{2}$,-$\frac{m}{2}$),半径r=$\sqrt{\frac{{m}^{2}}{2}-2}$,
由题意可知P在圆外时,过点P可作圆x2+y2+mx+my+2=0的两条切线,
所以d>r即1+1+m+m+2>0,且$\frac{{m}^{2}}{2}$-2>0,解得:m>2,
则m的取值范围是(2,+∞).
故选A.
点评 此题考查学生掌握点与圆的位置的判别方法,灵活运用两点间的距离公式化简求值,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.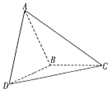 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
17.一个几何体的三视图如图所示(三个正方形的边长都是2),则该几何体的表面积是( )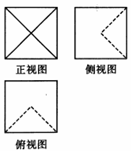

| A. | $20+4\sqrt{2}$ | B. | $24+4\sqrt{2}$ | C. | 24 | D. | 28 |
2.在下列函数中,最小值是2的是( )
| A. | y=$\frac{x}{2}$+$\frac{2}{x}$ | B. | y=lgx+$\frac{1}{lgx}$(1<x<10) | ||
| C. | y=3x+3-x(x∈R) | D. | y=sinx+$\frac{1}{sinx}$(0$<x<\frac{π}{2}$) |
 如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.
如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.