题目内容
5.已知等比数列的前三项分别是a-1,a+1,a+4,则数列{an}的通项公式为( )| A. | an=4×($\frac{3}{2}$)n | B. | an=4×($\frac{3}{2}$)n-1 | C. | an=4×($\frac{2}{3}$)n | D. | an=4×($\frac{2}{3}$)n-1 |
分析 根据等比中项的性质列出方程求出a的值,代入前三项求出公比q的值,代入等比数列的通项公式求出an.
解答 解:∵等比数列{an}的前三项为a-1,a+1,a+4,
∴(a+1)2=(a-1)(a+4),解得a=5,
则等比数列{an}的前三项为4,6,9,∴公比q=$\frac{2}{3}$,
∴an=4×($\frac{3}{2}$)n-1,
故选:B
点评 本题考查等比中项的性质,等比数列的通项公式,属于基础题.

练习册系列答案
相关题目
16.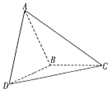 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
13.若0<a<b<1,c>1,则( )
| A. | ac>bc | B. | abc>bac | C. | logab>logba | D. | logac<logbc |
10.已知p>0,q>0,随机变量ξ的分布列如下:
若E(ξ)=$\frac{4}{9}$.则p2+q2=( )
| ξ | p | q |
| P | q | p |
| A. | $\frac{4}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | 1 |
17.一个几何体的三视图如图所示(三个正方形的边长都是2),则该几何体的表面积是( )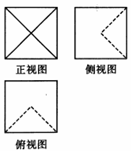

| A. | $20+4\sqrt{2}$ | B. | $24+4\sqrt{2}$ | C. | 24 | D. | 28 |
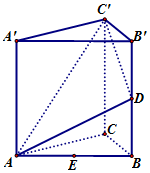 如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.
如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上. 如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.
如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.