题目内容
5.已知函数y=sin x的图象经过以下变换后得到y=f(x)的图象:先向右平移 $\frac{π}{4}$; 然后纵坐标不变,横坐标伸长为原来的2倍; 最后横坐标不变,纵坐标伸长为原来的3倍;(Ⅰ)写出函数y=f(x)的解析式,并求其单调增区间;
(Ⅱ)用“五点法”在给定的坐标系中作出函数的一个周期的图象.
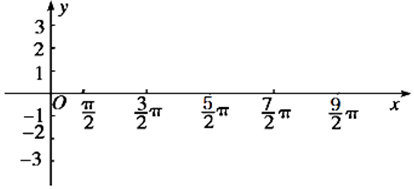
分析 (Ⅰ)根据三角函数图象平移法则,得出函数y=f(x)的解析式,利用正弦函数的图象与性质求出f(x)的单调增区间;
(Ⅱ)利用列表、描点、连线的方法得出函数在一个周期的图象.
解答 解:(Ⅰ)函数y=sin x的图象向右平移 $\frac{π}{4}$,得到y=sin(x-$\frac{π}{4}$)的图象;
纵坐标不变,横坐标伸长为原来的2倍,得到y=sin($\frac{1}{2}$x-$\frac{π}{4}$)的图象;
横坐标不变,纵坐标伸长为原来的3倍,得到y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)的图象;
∴函数y=f(x)=3sin($\frac{1}{2}$x-$\frac{π}{4}$);
令-$\frac{π}{2}$+2kπ≤$\frac{1}{2}$x-$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{π}{2}$+4kπ≤x≤$\frac{3π}{2}$+4kπ,k∈Z,
∴f(x)的单调增区间为[-$\frac{π}{2}$+4kπ,$\frac{3π}{2}$+4kπ],k∈Z;
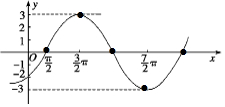
(Ⅱ)列表如下;
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) | 0 | 3 | 0 | -3 | 0 |
点评 本题考查了三角函数的图象与性质的应用问题,也l考查了图象平移与五点法画图的问题,是基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
16.已知等差数列{an}中,a3,a7是方程x2-8x+9=0的两个根,则a5等于( )
| A. | -3 | B. | 4 | C. | -4 | D. | 3 |
10.在空间直角坐标系中,A(0,2,4),B(1,4,6),则|AB|等于( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3 |
17.1340°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
15.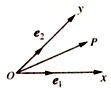 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |