题目内容
2. 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )
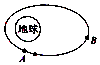
神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )| A. | d1+d2+R | B. | d2-d1+2R | C. | d2+d1-2R | D. | d1+d2 |
分析 设椭圆的方程,根据题意可得:$\left\{\begin{array}{l}{{d}_{1}+R=a-c}\\{{d}_{2}+R=a+c}\end{array}\right.$,则2a=d1+d2+2R,利用椭圆的定义可知神秘信号的最短距离为丨PF1丨+丨PF2丨-2R=2a-2R=d1+d2.
解答 解:设椭圆的方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),半焦距为c,
两焦点分别为F1,F1,运行中的航天员为P,
由已知可得:$\left\{\begin{array}{l}{{d}_{1}+R=a-c}\\{{d}_{2}+R=a+c}\end{array}\right.$,则2a=d1+d2+2R,
神秘信号的最短距离为丨PF1丨+丨PF2丨-2R=2a-2R=d1+d2,
神秘信号传导的最短距离d1+d2,
故选D.
点评 本题考查椭圆的性质,考查椭圆定义的物理应用,考查利用椭圆方程解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
17.设复数z=1-$\sqrt{3}$i(i是虚数单位),则$\frac{2}{z•\overline{z}}$+$\frac{i}{1-i}$=( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}$i |
14.设x∈R,则“x<4”是“x2-2x-8<0”的( )
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.△ABC的内角A,B,C的对边分别是a,b,c,若a2=(b+c)2-4,△ABC的面积为$\sqrt{3}$,则A等于( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
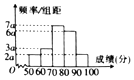 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示. 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.