题目内容
10.设{an}是由正数组成的等比数列,Sn是{an}的前n项和.已知a2a4=16,S3=28,则a1a2…an最大时,n的值为3或4.分析 由题意列式求出等比数列的首项和公比,求出等比数列的通项公式,代入a1a2…an,然后结合二次函数求值得答案.
解答 解:∵{an}是由正数组成的等比数列,Sn是{an}的前n项和.a2a4=16,S3=28,
∴$\left\{\begin{array}{l}{{a}_{1}q•{a}_{1}{q}^{3}=16}\\{\frac{{a}_{1}(1-{q}^{3})}{1-q}=28}\\{q>0}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=8}\\{q=\frac{1}{2}}\end{array}\right.$.
∴${a}_{n}=8•(\frac{1}{2})^{n-1}={2}^{4-n}$.
则a1a2…an=2(4-1)+(4-2)+…+(4-n)=${2}^{-\frac{{n}^{2}}{2}+\frac{7n}{2}}$.
∴当n=3或n=4时,a1a2…an取最大值.
故答案为:3或4.
点评 本题考查等比数列的通项公式,考查等差数列的前n项和,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标,若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为$\frac{5}{6}$,那么9个空气净化器中甲、乙品牌个数分布可能是( )
| A. | 甲品牌1个,乙品牌8个 | B. | 甲品牌2个,乙品牌7个 | ||
| C. | 甲品牌3个,乙品牌6个 | D. | 甲品牌4个,乙品牌5个 |
5.若双曲线x2+my2=2的虚轴长为2,则该双曲线的焦距为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
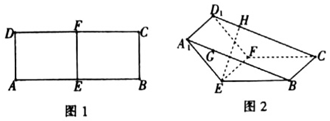 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.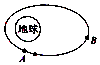 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )
神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )