题目内容
已知双曲线C的中心在原点,焦点在x轴上,右准线为l:x=
,一条渐近线的方程是y=
x.过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是弦PQ的中点.
(1)求双曲线C的方程;
(2)若在l的左侧能作出直线m:x=a,使点R在直线m上的射影S满足
•
=0,当点P在曲线C上运动时,求a的取值范围.
| 1 |
| 2 |
| 3 |
(1)求双曲线C的方程;
(2)若在l的左侧能作出直线m:x=a,使点R在直线m上的射影S满足
| PS |
| QS |
考点:圆锥曲线的综合
专题:向量与圆锥曲线
分析:(1)设出渐近线方程是y=
x的双曲线方程为
-
=1(λ>0),求出其右准线方程,由右准线为l:x=
求得λ的值,则双曲线C的方程可求;
(2)由S满足
•
=0,得△PSQ是直角三角形.由点R到直线m:x=a(a≤
)的距离为|RS|=
=xR-a,结合椭圆第二定义得|PQ|=4xR-2,联立后再由R的横坐标大于等于2求解实数a的取值范围.
| 3 |
| x2 |
| λ |
| y2 |
| 3λ |
| 1 |
| 2 |
(2)由S满足
| PS |
| QS |
| 1 |
| 2 |
| |PQ| |
| 2 |
解答:
解:(1)由渐近线的方程是y=
x,可设双曲线C的方程为
-
=1(λ>0),
则它的右准线方程为x=
,即x=
.
∵右准线为l:x=
,
∴
=1,则λ=1,
∴所求双曲线C的方程是x2-
=1;
(2)∵点R在直线m上的射影S满足
•
=0,
∴PS⊥QS,即△PSQ是直角三角形.
∴点R到直线m:x=a(a≤
)的距离为|RS|=
=xR-a,
即|PQ|=2xR-2a…①
又由椭圆第二定义知
=
=2.
∴|PQ|=|PF2|+|F2Q|=2(xP-xQ-1)=4xR-2…②
将②代入①,得xR=1-a.
又P、Q是过右焦点F2的一条弦,且P、Q均在双曲线C的右支上,R是弦PQ的中点.
∴xR≥2,
即1+a≥2,∴a≤-1.
故所求a的取值范围是a≤-1.
| 3 |
| x2 |
| λ |
| y2 |
| 3λ |
则它的右准线方程为x=
| λ | ||
2
|
| ||
| 2 |
∵右准线为l:x=
| 1 |
| 2 |
∴
| λ |
∴所求双曲线C的方程是x2-
| y2 |
| 3 |
(2)∵点R在直线m上的射影S满足
| PS |
| QS |
∴PS⊥QS,即△PSQ是直角三角形.
∴点R到直线m:x=a(a≤
| 1 |
| 2 |
| |PQ| |
| 2 |
即|PQ|=2xR-2a…①
又由椭圆第二定义知
| |PF2| | ||
xP-
|
| |F2Q| | ||
xQ-
|
∴|PQ|=|PF2|+|F2Q|=2(xP-xQ-1)=4xR-2…②
将②代入①,得xR=1-a.
又P、Q是过右焦点F2的一条弦,且P、Q均在双曲线C的右支上,R是弦PQ的中点.
∴xR≥2,
即1+a≥2,∴a≤-1.
故所求a的取值范围是a≤-1.
点评:本题考查了双曲线标准方程的求法,考查了直线与双曲线的位置关系,考查了数学转化思想方法,综合考查了学生分析问题和解决问题的能力,属高考试卷中的压轴题.

练习册系列答案
相关题目
函数y=x3-x2-x的单调递增区间为( )
A、(-∞,-
| ||
B、[-
| ||
C、(-∞,-
| ||
D、[-1,
|
某几何体的三视图如图所示,则此几何体的体积是( )


A、
| ||
| B、6π | ||
C、
| ||
D、
|
在平面直角坐标系中,点A、B分别是x轴、y轴上两个动点,又有一定点M(3,4),则|MA|+|AB|+|BM|的最小值是( )
| A、10 | B、11 | C、12 | D、13 |
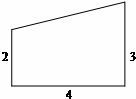 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是 如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)
如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)