题目内容
18.已知定义在(-∞,3]上单调减函数f(x)使得f(1+sin2x)≤f(a-2cosx)对一切实数x都成立,求a的取值范围.分析 根据函数单调性的性质将不等式进行转化,利用参数分离法转化为求函数的最值,结合一元二次函数的性质进行求解即可.
解答 解:∵定义在(-∞,3]上单调减函数f(x)使得f(1+sin2x)≤f(a-2cosx)对一切实数x都成立,
∴等价为1+sin2x≥a-2cosx,
即a≤1+sin2x+2cosx恒成立,且a-2cosx≤3,即a≤3+2cosx,则a≤1,
设h(x)=1+sin2x+2cosx,则h(x)=1+sin2x+2cosx=2-cos2x+2cosx=-(cosx-1)2+1,
∵-1≤cosx≤1,∴-3≤h(x)≤1,
则a≤-3,∵a≤1,
∴a≤-3.
即实数a的取值范围是(-∞,-3]
点评 本题主要考查不等式恒成立问题,根据函数单调性的性质将不等式进行转化,结合一元二次函数的性质求出函数的最值是解决本题的关键.

练习册系列答案
相关题目
8.若复数z满足z(6-8i)=|8+6i|(i是虚数单位),则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | 4 | C. | -$\frac{4}{5}$ | D. | -4 |
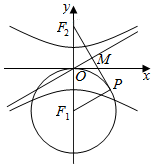 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )