题目内容
3. 如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为
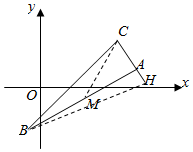
如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为x-2y-5=0.AB边上的中线CM所在直线方程为2x-y-5=0.
(Ⅰ)求AC边所在直线的方程;
(Ⅱ)求顶点C的坐标.
分析 (Ⅰ)由两直线相互垂直时的斜率的关系,求得直线AC的斜率,再由点斜式方程可得直线AC的方程;
(Ⅱ)由直线AC与中线CM交于C,联立直线AC的方程和CM的方程,解方程组,即可得到所求C的坐标.
解答  解:(Ⅰ)∵点H在直线x-2y-5=0,
解:(Ⅰ)∵点H在直线x-2y-5=0,
∵BH⊥AC,
∴kAC•kBH=-1,可得kAC=-$\frac{1}{\frac{1}{2}}$=-2,
则直线AC的方程为y-1=-2(x-5),
即为2x+y-11=0;
(Ⅱ)由直线AC与CM交于C,
解方程组$\left\{\begin{array}{l}{2x+y-11=0}\\{2x-y-5=0}\end{array}\right.$,
可得x=4,y=3,
即C(4,3).
点评 本题考查学生掌握两直线垂直时满足斜率乘积为-1的条件,会求两直线的交点坐标,以及会根据斜率和一点坐标写出直线的一般式方程.

练习册系列答案
相关题目
11.设集合M={x|x2>4},N={x|-1<x≤3},则M∩N=( )
| A. | (-2,3] | B. | [2,3] | C. | (2,3] | D. | (2,3) |
11.已知向量 $\overrightarrow a=(0,1),\overrightarrow b=(-1,1)$,则$\overrightarrow a•\overrightarrow b$=1.
18.设命题p:?x∈R,x02>lnx,则¬p为( )
| A. | ?x0∈R,x02>lnx0 | B. | ?x0∈R,x02≥lnx0 | C. | ?x0∈R,x02<lnx0 | D. | ?x0∈R,x02≤lnx0 |
8.集合M={x|y=$\sqrt{1-x}$},N={x|y=ln(4-x2)},则M∩N=( )
| A. | (-2,1] | B. | (1,2) | C. | (-∞,1] | D. | (-2,1) |
15.函数f(x)=x2+3x-4 的单调递增区间是( )
| A. | (-∞,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,+∞) | C. | [$\frac{3}{2}$,4) | D. | (-1,$\frac{3}{2}$] |
12. 从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
 从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )| A. | 甲种玉米比乙种玉米不仅长得高而且长得整齐 | |
| B. | 乙种玉米比甲种玉米不仅长得高而且长得整齐 | |
| C. | 甲种玉米比乙种玉米长得高但长势没有乙整齐 | |
| D. | 乙种玉米比甲种玉米长得高但长势没有甲整齐 |
1.设等差数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n成等差数列,类比以上结论,设等比数列{bn}的前
n项积为Tn,则( )
n项积为Tn,则( )
| A. | Tn,T2n,T3n成等比数列 | B. | Tn,T2n-Tn,T3n-T2n成等差数列 | ||
| C. | Tn,$\frac{{T}_{2n}}{{T}_{n}}$,$\frac{{T}_{3n}}{{T}_{2n}}$成等比数列 | D. | Tn,T2n-Tn,T3n-T2n成等比数列 |