题目内容
12.已知函数f(x)的导函数f'(x)是二次函数,且y=f'(x)的图象关于y轴对称,f'(3)=0,若f(x)的极大值与极小值之和为4,则f(0)=2.分析 设出函数的解析式f(x)=$\frac{1}{3}a{x}^{3}-9ax+b$,求出函数的导数,利用函数的极值关系求解b,然后推出结果.
解答 解:函数f(x)的导函数f'(x)是二次函数,且y=f'(x)的图象关于y轴对称,f'(3)=0,则f'(-3)=0,
可设导函数为:f'(x)=ax2-9a,函数的解析式设为:f(x)=$\frac{1}{3}a{x}^{3}-9ax+b$,
若f(x)的极大值与极小值之和为4,则f(3)+f(-3)=4,
可得:9a-27a-9a+27a+2b=4,解得b=2.
则f(0)=b=2.
故答案为:2.
点评 本题考查函数的极值以及函数的导数的应用,函数的奇偶性的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
5.若点M(a,b)在函数y=-x2+3lnx的图象上,点N(c,d)在函数y=x-2的图象上,则$\sqrt{(a+c)^{2}+(b+d)^{2}}$的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
3.如图,圆O的半径为2,点A满足OA=1.设点B,C为圆O上的任意两点,则$\overrightarrow{AC}•\overrightarrow{BC}$的最小值是( )


| A. | 2 | B. | 0 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
17.若复数z=-9-i,则$\overrightarrow{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
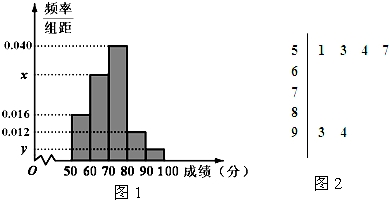
 某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是700.
某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是700. 执行如图所示的程序框图,若输出的y=6,则输入的x=-6或3.
执行如图所示的程序框图,若输出的y=6,则输入的x=-6或3.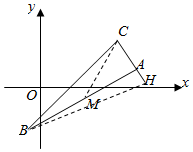 如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为
如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为