题目内容
已知复数z满足z•(i-1)=2i,则z的共轭复数
为( )
. |
| z |
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的除法运算可求得z=1-i,于是可得答案.
解答:
解:∵z•(i-1)=2i,
∴z=
=1-i,
∴
=1+i,
故选:B.
∴z=
| 2i(-1-i) |
| (-1+i)(-1-i) |
∴
. |
| z |
故选:B.
点评:本题考查复数代数形式的乘除运算,分母实数化是关键,考查运算求解能力,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知复数z满足
=1-2i,则z=( )
| z |
| 1+2i |
| A、-5 | B、5 | C、-3 | D、3 |
设集合A={x|y=lgx},B={x|x≤1},则A∩B=( )
| A、(0,+∞) |
| B、[1,+∞) |
| C、(0,1] |
| D、(-∞,1] |
已知不等式
<0的解集为P,若x0∈P,则“|x0|<1“的概率为( )
| x-5 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若命题甲:“p且q是真命题”,命题乙:“p或q是真命题”,则命题甲是命题乙的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
已知Sn=1+
+
+…+
,那么Sn的取值范围是( )
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
A、(1,
| ||
| B、[1,2) | ||
| C、(2,5) | ||
| D、(5,+∞) |
将长方体截去一个四棱锥,得到几何体如图所示,则该几何体的正视图为( )


A、 |
B、 |
C、 |
D、 |
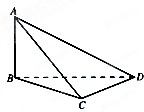 如图,已知AB⊥平面BCD,BC⊥CD,则该三棱锥中互相垂直的平面有
如图,已知AB⊥平面BCD,BC⊥CD,则该三棱锥中互相垂直的平面有