题目内容
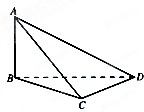如图，已知AB⊥平面BCD，BC⊥CD，则该三棱锥中互相垂直的平面有（1）平面ABC⊥平面BCD
（2）平面ACD⊥平面ABD
（3）平面ABD⊥平面ABC
（4）平面BCD⊥平面ABD
（5）平面ACD⊥平面ABC．
考点：平面与平面垂直的判定
专题：综合题,空间位置关系与距离
分析：先根据线面垂直的判定定理判断线面垂直的情况，再根据面面垂直的判定定理判断面面垂直的情况．
解答：
解：∵AB⊥平面BCD，AB?平面ABC，AB?平面ABD，
∴平面ABC⊥平面BCD；
平面ABD⊥平面BCD，
∵BC⊥CD，AB⊥CD，AB∩BC=B，
∴CD⊥平面ABC，CD?平面ACD
∴平面ACD⊥平面ABC．
故答案为：（1）（4）（5）．
∴平面ABC⊥平面BCD；
平面ABD⊥平面BCD，
∵BC⊥CD，AB⊥CD，AB∩BC=B，
∴CD⊥平面ABC，CD?平面ACD
∴平面ACD⊥平面ABC．
故答案为：（1）（4）（5）．
点评：本题考查棱锥的结构特征，求解本题的关键是对棱锥中的点线面的位置关系有着比较熟悉的了解，且能根据其已知的位置关系作出一些判断得出新的结论，本题考查了空间想像能力以及推理论证的能力．空间问题问题平面问题相互转化的能力．
练习册系列答案
相关题目
某学校高二年级学生有30个班，每个班的56名同学都是从1到56编的号码，为了交流学习经验，要求每班号码为16的同学留下进行交流，这里运用的是（ ）
| A、分层抽样 | B、抽签抽样 |
| C、随机抽样 | D、系统抽样 |
已知复数z满足z•（i-1）=2i，则z的共轭复数
为（ ）
. |
| z |
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |
若i为虚数单位，则复数
等于（ ）
| i | ||
|
A、-
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|