题目内容
6.在△ABC中,D为BC边上一点,且满足$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),BC=10,AD=12,且$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,则$\overrightarrow{AD}$•$\overrightarrow{AC}$=( )| A. | 144 | B. | 100 | C. | 169 | D. | 60 |
分析 由题意可得△ABC为等腰三角形,根据勾股定理求出AC=13,再根据向量的数量积公式计算即可.
解答 解:D为BC边上一点,且满足$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴D为BC的中点,
∵$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,
∴$\overrightarrow{AD}$⊥$\overrightarrow{BC}$,
∴AB=AC,
∵BC=10,AD=12,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=13,
∴cos∠DAC=$\frac{12}{13}$,
∴$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AD}$|•|$\overrightarrow{AC}$|•cos∠DAC=13×12×$\frac{12}{13}$=144,
故选:A
点评 本题考查了向量的加减的几何意义和向量的垂直和向量的数量积公式,判断出AB=AC是关键,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
17.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
1.已知z=$\frac{1-3i}{3+i}$(i为虚数单位),则z的共轭复数的虚部为( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
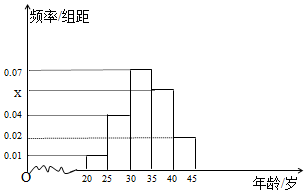 为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示. 机器人AlphaGo(阿法狗)在下围棋时,令人称道算法策略是:每一手棋都能保证在接下来的十步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.下面的算法上算法是寻找“a1,a2,…,a10”中“比较大的数t”.现输入正整数“42,61,80,12,79,18,82,57,31,18”,从左到右依次为a1,a2,…,a10,其中最大的数记为T,则T-t=( )
机器人AlphaGo(阿法狗)在下围棋时,令人称道算法策略是:每一手棋都能保证在接下来的十步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.下面的算法上算法是寻找“a1,a2,…,a10”中“比较大的数t”.现输入正整数“42,61,80,12,79,18,82,57,31,18”,从左到右依次为a1,a2,…,a10,其中最大的数记为T,则T-t=( )