题目内容
9.定义在 R 上的奇函数 f (x) 满足 f (2+x )=f (2-x),且 f (1)=1,则 f (2017)=( )| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
分析 求出函数的周期,然后利用周期性以及函数的奇偶性求解即可.
解答 解:定义在R上的奇函数f(x)满足 f (2+x )=f (2-x),且 f (1)=1,
可得f(x+4)=f(-x)=-f(x),f(x+8)=f(x),T=8,
f(2017)=f(1)=1.
故选B.
点评 本题考查函数的奇偶性以及函数的周期性的应用,考查计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.函数$y=sin(2x+\frac{π}{3})$的图象经过下列平移,可以得到函数$y=cos(2x+\frac{π}{6})$图象的是( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
20.已知$\overline{z}$为复数z的共轭复数,且(1-i)z=1+i,则$\overline{z}$为( )
| A. | -i | B. | i | C. | 1-i | D. | 1+i |
17.已知 x>1,y>1,且 lg x,$\frac{1}{4}$,lg y 成等比数列,则 xy 有( )
| A. | 最小值10 | B. | 最小值$\sqrt{10}$ | C. | 最大值10 | D. | 最大值 $\sqrt{10}$ |
4.已知λ∈R,向量$\overrightarrow{a}$=( 3,λ ),$\overrightarrow{b}$=(λ-1,2),则“λ=$\frac{3}{5}$”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知点M(0,$\sqrt{15}$)及抛物线y2=4x上一动点N(x,y),则x+|MN|的最小值为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 4 |
17.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
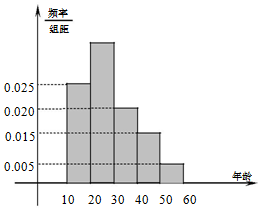 •滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.
•滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.