题目内容
4.已知二次函数y=f(x)的图象向上平移2个单位长度,再向右平移1个单位长度,得到函数y=-2x2+4x+1的图象,则f(x)的函数解析式为( )| A. | f(x)=-2x2+1 | B. | f(x)=-2(x+1)2+2 | C. | f(x)=-2(x-3)2+4 | D. | f(x)=-2(x-2)2+5 |
分析 根据函数的平移变换规律即可得出.
解答 解:设g(x)=-2x2+4x+1,
∵g(x)是由f(x)的图象向上平移2个单位长度,再向右平移1个单位长度得到的,
∴f(x)=g(x+1)-2=-2(x+1)2+4(x+1)-1=-2x2+1.
故选:A.
点评 本题考查了函数图象的平移变换规律,属于基础题.

练习册系列答案
相关题目
16.下列四条直线,其倾斜角最大的是( )
| A. | x+2y+3=0 | B. | 2x-y+1=0 | C. | x+y+1=0 | D. | x+1=0 |
17.已知 x>1,y>1,且 lg x,$\frac{1}{4}$,lg y 成等比数列,则 xy 有( )
| A. | 最小值10 | B. | 最小值$\sqrt{10}$ | C. | 最大值10 | D. | 最大值 $\sqrt{10}$ |
1.已知点M(0,$\sqrt{15}$)及抛物线y2=4x上一动点N(x,y),则x+|MN|的最小值为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 4 |
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
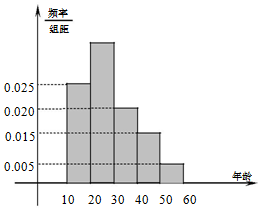 •滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.
•滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.