题目内容
5.已知抛物线C:y2=2px(p>0)的焦点为F,$A({0\;\;,\;\;\sqrt{3}})$,抛物线C上的点B满足AB⊥AF,且|BF|=4,则p=2或6.分析 求出直线AB的方程,与抛物线方程联立,求出B的横坐标,利用抛物线的定义,即可得出结论.
解答 解:由题意,kAF=-$\frac{2\sqrt{3}}{p}$,
∴直线AB的方程为y=$\frac{p}{2\sqrt{3}}$x+$\sqrt{3}$,
代入y2=2px,可得p2x2-12px+36=0,∴x=$\frac{6}{p}$,
∵|BF|=4,
∴$\frac{6}{p}$+$\frac{p}{2}$=4,∴p=2或6,
故答案为2或6.
点评 本题考查抛物线的定义,考查直线与抛物线位置关系的运用,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
15.设a∈R,“a>0”是“$\frac{1}{a}>0$”的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既非充分也非必要 |
16.已知集合A={x|x2-2x-3≤0},B={x|x>0},则A∩B=( )
| A. | (0,3] | B. | (0,3) | C. | [0,3] | D. | [3,+∞) |
20.在△ABC中,∠B=90°,$\overrightarrow{AB}=({1\;\;,\;\;-2})$,$\overrightarrow{AC}=({3\;\;,\;\;λ})$,则λ=( )
| A. | -1 | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
10.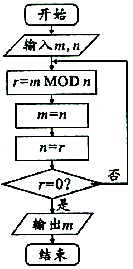 如图所示,程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为2016,612,则输出的m=( )
如图所示,程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为2016,612,则输出的m=( )
 如图所示,程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为2016,612,则输出的m=( )
如图所示,程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为2016,612,则输出的m=( )| A. | 0 | B. | 36 | C. | 72 | D. | 180 |
15.已知m,n是两条不同的直线,α,β是两个不重合的平面.命题p:若α∩β=m,m⊥n,则n⊥α;命题q:若m∥α,m?β,α∩β=n,则m∥n.那么下列命题中的真命题是( )
| A. | p∧q | B. | p∨¬q | C. | ¬p∧q | D. | ¬p∧¬q |