题目内容
在空间直角坐标系O-xyz中,坐标原点为O,P点坐标为(x,y,z).
(Ⅰ)若点P在x轴上,且坐标满足|2x-5|≤3,求点P到原点O的距离的最小值;
(Ⅱ)若点P到坐标原点O的距离为2
,求x+y+z的最大值.
(Ⅰ)若点P在x轴上,且坐标满足|2x-5|≤3,求点P到原点O的距离的最小值;
(Ⅱ)若点P到坐标原点O的距离为2
| 3 |
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:综合题,推理和证明,不等式
分析:(Ⅰ)利用绝对值不等式,求出x的范围,即可求点P到原点O的距离的最小值;
(Ⅱ)点P到坐标原点O的距离为2
,故x2+y2+z2=12,由柯西不等式,得(x2+y2+z2)(12+12+12)≥(x+y+z)2,即可求x+y+z的最大值.
(Ⅱ)点P到坐标原点O的距离为2
| 3 |
解答:
解:(Ⅰ)由点P在x轴上,所以P(x,0,0),
又坐标满足|2x-5|≤3,所以-3≤2x-5≤3,…(2分)
解得1≤x≤4,…(3分)
所以点P到原点O的距离的最小值为1..…(4分)
(Ⅱ)由点P到坐标原点O的距离为2
,
故x2+y2+z2=12,…(5分)
由柯西不等式,得(x2+y2+z2)(12+12+12)≥(x+y+z)2,…(6分)
即(x+y+z)2≤36,
所以x+y+z的最大值为6,当且仅当x=y=z=2时取最大.…(7分)
又坐标满足|2x-5|≤3,所以-3≤2x-5≤3,…(2分)
解得1≤x≤4,…(3分)
所以点P到原点O的距离的最小值为1..…(4分)
(Ⅱ)由点P到坐标原点O的距离为2
| 3 |
故x2+y2+z2=12,…(5分)
由柯西不等式,得(x2+y2+z2)(12+12+12)≥(x+y+z)2,…(6分)
即(x+y+z)2≤36,
所以x+y+z的最大值为6,当且仅当x=y=z=2时取最大.…(7分)
点评:本题主要考查绝对值不等式、柯西不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想.

练习册系列答案
相关题目
若向量
、
满足
+
=(2,-1),
=(1,2),则向量
与
的夹角等于( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、135° | B、120° |
| C、60° | D、45° |
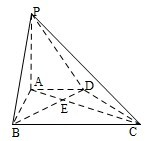 四棱锥P-ABCD中,ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥面ABCD,PA=3,AD=2,AB=2
四棱锥P-ABCD中,ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥面ABCD,PA=3,AD=2,AB=2