题目内容
若数列{an}的各项按如下规律排列:
,
,
,
,
,
,
,
,
,
,…,
,
,…,
,…,则a2012=( )
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 4 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 4 |
| n+1 |
| 1 |
| n+1 |
| 2 |
| n+1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:归纳推理
专题:规律型
分析:由已知先找到数列{an}的项数的规律,按分子进行分组后,当分子为n+1时,该组共有n项,第k项的分子为k,此时数列{an}共有1+2+…+n=
项,由此分析a2012属于哪一组的哪一项,即可得到答案.
| n(n+1) |
| 2 |
解答:
解:数列{an}的各项按如下规律排列:
当当分子为n+1时,该组共有n项,第k项的分子为k,此时数列{an}共有1+2+…+n=
项,
∵当n=62时,
=1953<2012,n=63时,
=2016>2012,
故2012在分子为64的组内,
且为该组的2012-1953=59项,
故a2012=
,
故选:A
当当分子为n+1时,该组共有n项,第k项的分子为k,此时数列{an}共有1+2+…+n=
| n(n+1) |
| 2 |
∵当n=62时,
| 63×62 |
| 2 |
| 64×63 |
| 2 |
故2012在分子为64的组内,
且为该组的2012-1953=59项,
故a2012=
| 64 |
| 59 |
故选:A
点评:本题考查的知识点是归纳推理,分析其排列规律和项数规律是解决问题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
关于以下四个命题,不正确的是( )
①若函数y=2x的定义域是{x|x≤0},则它的值域为{y|y≤1}
②若函数y=
的定义域是{x|x>2},则它的值域为{y|y<
}
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
①若函数y=2x的定义域是{x|x≤0},则它的值域为{y|y≤1}
②若函数y=
| 1 |
| x |
| 1 |
| 2 |
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
在下列命题中,正确的是( )
A、若|
| ||||||||
B、若|
| ||||||||
C、若
| ||||||||
D、若
|
若sin2θ-1+(
+1)i是纯虚数,则θ的值为( )
| 2 |
A、2kπ-
| ||||
B、kπ+
| ||||
C、2kπ±
| ||||
D、
|
关于曲线的对称性的论述正确的是( )
| A、方程x2+xy+y2=0的曲线关于X轴对称 |
| B、方程x3+y3=0的曲线关于Y轴对称 |
| C、方程x2-xy+y2=10的曲线关于原点对称 |
| D、方程x3-y3=8的曲线关于原点对称 |
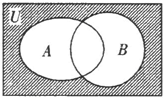 设全集U={1,2,3,4,5,6,7,8},集合A={2,4,5,7},B={1,4,7,8},那么如图所示的阴影部分所表示的集合是( )
设全集U={1,2,3,4,5,6,7,8},集合A={2,4,5,7},B={1,4,7,8},那么如图所示的阴影部分所表示的集合是( )| A、{3,6} |
| B、{4,7} |
| C、{1,2,4,5,7,8} |
| D、{1,2,3,5,6,8} |
三个实数a,b,c依次成公差不为零的等差数列,且a,c,b成等比数列,则
的值是( )
| a |
| b |
| A、-2 | B、2 | C、4 | D、-4 |