题目内容
17.若cosα=$\frac{3}{5}$,tanα<0,则sinα=-$\frac{4}{5}$.分析 由条件利用同角三角函数的基本关系求得sinα的值.
解答 解:∵cosα=$\frac{3}{5}$,tanα<0,则sinα<0,且sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{4}{5}$,
故答案为:-$\frac{4}{5}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的两点A,B,若|AF|=4|FB|,则k的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{3}{4}\sqrt{2}$ | C. | $\frac{{\sqrt{17}}}{4}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
6.若复数$\frac{a-3i}{1+i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | 3 | B. | -3 | C. | 0 | D. | $\frac{3}{2}$ |
7.函数$f(x)=\sqrt{1-x}+{2^x}$的定义域为( )
| A. | (0,1) | B. | (0,1] | C. | (-∞,1] | D. | [1,+∞) |
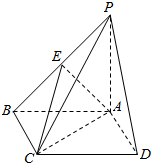 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.