题目内容
15.已知$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,定义:$\overrightarrow{a}$在$\overrightarrow{b}$方向上的“假投影”为|$\overrightarrow{a}$|$\overrightarrow{a}$cosθ,记为J($\overrightarrow{a}$,$\overrightarrow{b}$),若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,3),则|J($\overrightarrow{a}$,$\overrightarrow{b}$)|=$\frac{\sqrt{2}}{2}$.分析 $\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ根据向量的夹角公式求出cosθ,|$\overrightarrow{a}$|,再根据新定义即可求出答案.
解答 解:∵$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,3),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×(-1)+1×3=1,|$\overrightarrow{a}$|=$\sqrt{5}$,$\overrightarrow{b}$=$\sqrt{10}$,
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{1}{\sqrt{5}•\sqrt{10}}$=$\frac{\sqrt{2}}{10}$
∴J($\overrightarrow{a}$,$\overrightarrow{b}$)=|$\overrightarrow{a}$|$\overrightarrow{a}$cosθ=$\sqrt{5}$$•\frac{\sqrt{2}}{10}$•$\overrightarrow{a}$=$\frac{\sqrt{10}}{10}$$•\overrightarrow{a}$,
∴|J($\overrightarrow{a}$,$\overrightarrow{b}$)|=$\frac{\sqrt{10}}{10}$•$\sqrt{5}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题考查了向量的数量积的运算和向量的夹角公式以及新定义,属于中档题.

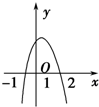
| A. | (-2,1) | B. | (0,3) | C. | (-1,2] | D. | (-∞,0)∪(3,+∞) |
| A. | {恰好2个红色的变形金刚} | B. | {恰好2个黑色的变形金刚} | ||
| C. | {恰好2个白色的变形金刚} | D. | {至少1个红色的变形金刚} |
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
| A. | -i | B. | 11 | C. | 1 | D. | -1 |
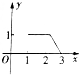
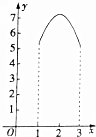
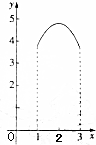
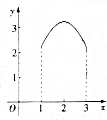
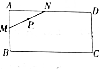 如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )
如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )