题目内容
4.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-1≤0}\\{x≥0}\\{y≥0}\end{array}\right.$,若0≤ax+by≤2,则$\frac{b+2}{a+1}$的最大值是4.分析 作出不等式组对应的平面区域,利用线性规划的知识先求出a,b的范围,然后利用斜率的几何意义进行求解即可.
解答 解:作出不等式组对应的平面区域如图: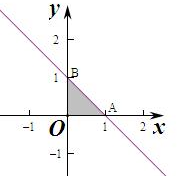 若0≤ax+by≤2,恒成立,
若0≤ax+by≤2,恒成立,
则只需要A(1,0),B(0,1),(0,0)满足不等式即可,
则$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\end{array}\right.$,$\frac{b+2}{a+1}$的几何意义是区域内的点到(-1,-2)的斜率,
作出不等式组对应的平面区域如图: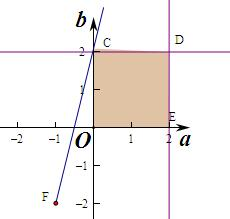
则CF的斜率最大,此时C(0,2),
则$\frac{b+2}{a+1}$的最大值为$\frac{2+2}{0+1}=4$,
故答案为:4.
点评 本题主要考查线性规划的应用,利用数形结合进行转换是解决本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
12.下列四个选项中,表示终边在第二、四象限角平分线上的角的集合是( )
| A. | {β|β=-$\frac{π}{4}$} | B. | {β|β=$\frac{3π}{4}$} | C. | {β|β=-$\frac{π}{4}$或$\frac{3π}{4}$} | D. | {β|β=$\frac{3π}{4}$+kπ,k∈Z} |
19.已知在公比大于1的等比数列{an}中,a3+a6=28,a4•a5=27,则数列{an}的前6项和为( )
| A. | $\frac{182}{9}$ | B. | $\frac{364}{9}$ | C. | 20 | D. | 40 |
11.设a2+b2=1,x2+y2=4,则ax+by的最大值是( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 4 | D. | 8 |