题目内容
已知不等式组
表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A、B,当∠APB最大时,cos∠APB=( )
|
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据数形结合求确定当α最小时,P的位置,利用余弦函数的倍角公式,即可得到结论.
解答:
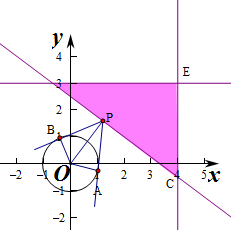
解:作出不等式组对应的平面区域如图,要使∠APB最大,
则P到圆心的距离最小即可,
由图象可知当OP垂直直线3x+4y-10=0,
 此时|OP|=
此时|OP|=
=
=2,|OA|=1,
设∠APB=α,则∠APO=
,即sin
=
=
,
此时cosα=1-2sin2
=1-2×(
)2=1-
=
,
即cos∠APB=
.
故选:B
则P到圆心的距离最小即可,
由图象可知当OP垂直直线3x+4y-10=0,
 此时|OP|=
此时|OP|=| |-10| | ||
|
| 10 |
| 5 |
设∠APB=α,则∠APO=
| α |
| 2 |
| α |
| 2 |
| OA |
| OP |
| 1 |
| 2 |
此时cosα=1-2sin2
| α |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即cos∠APB=
| 1 |
| 2 |
故选:B
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键,要求熟练掌握两角和的倍角公式.

练习册系列答案
相关题目
程序框图如图所示:如果程序运行的结果S=1320,那么判断框中应填入( )


| A、K<10 | B、K≤10 |
| C、K<9 | D、K≤11 |
某程序框图如图所示,该程序运行后输出的k的值是( )


| A、3 | B、4 | C、5 | D、6 |
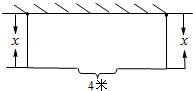 如图,某养殖户要建一个面积为800平方米的矩形养殖场,要求养殖场的一边利用旧墙(旧墙的长度大于4米),其他各边用铁丝网围成,且在矩形一边的铁丝网的正中间要留一个4米的进出口.设矩形的宽为x米,铁丝网的总长度为y米.
如图,某养殖户要建一个面积为800平方米的矩形养殖场,要求养殖场的一边利用旧墙(旧墙的长度大于4米),其他各边用铁丝网围成,且在矩形一边的铁丝网的正中间要留一个4米的进出口.设矩形的宽为x米,铁丝网的总长度为y米.
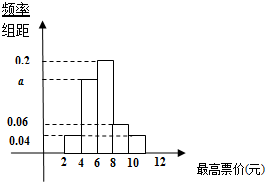 2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: