题目内容
13.一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”(如213),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“凹数”的有( )个.| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据题意,分2步进行分析:①、在1,2,3,4中任选3个,作为a,b,c,②、结合“凹数”的定义,将取出的3个数中最小的作为b,剩余2个数全排列,作为a、c;分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、在1,2,3,4中任选3个,作为a,b,c,有C43=4种情况,
②、由于“凹数”要求a>b,b<c,将取出的3个数中最小的作为b
,剩余2个数全排列,作为a、c,
有A22=2种情况,
则一共有4×2=8种情况,即有8个“凹数”;
故选:C.
点评 本题考查排列、组合的应用,关键是理解“凹数”的定义.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.函数f(x)=-4x3+3x+2(x∈[0,1])的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知动点M(x,y)的坐标满足方程$\sqrt{{{(y+5)}^2}+{x^2}}-\sqrt{{{(y-5)}^2}+{x^2}}=8$,则M的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1(x>0)$ | D. | $\frac{y^2}{16}-\frac{x^2}{9}=1(y>0)$ |
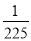 B.
B.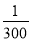 C.
C.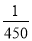 D.以上全不对
D.以上全不对 中,
中,  为直角三角形,且
为直角三角形,且 ,
, ,
, .求证:
.求证: .
.