题目内容
函数f(x)=(x+2)2(x-1)3的极大值点是( )
| A、x=-2或1 |
| B、x=-1或2 |
| C、x=-1 |
| D、x=-2 |
考点:利用导数研究函数的极值
专题:导数的概念及应用
分析:先求出函数的导数:f′(x)=(x-2)(x-2)2(5x+4),令f′(x)>0,解得:x>-
,或x<-2,从而得到x=-2是函数的极大值点.
| 4 |
| 5 |
解答:
解:∵f′(x)=(x-2)(x-2)2(5x+4),
令f′(x)>0,解得:x>-
,或x<-2,
∴函数f(x)在(-∞-2),(-
,+∞)上递增,在(-2,-
)上递减,
∴x=-2是函数的极大值点,
故选;D.
令f′(x)>0,解得:x>-
| 4 |
| 5 |
∴函数f(x)在(-∞-2),(-
| 4 |
| 5 |
| 4 |
| 5 |
∴x=-2是函数的极大值点,
故选;D.
点评:本题考察了函数的单调性,函数的极值问题,导数的应用,是一道基础题.

练习册系列答案
相关题目
sin62°cos32°-sin32°cos62°=( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设f(x)=
,若f(x)=x+a有且仅有三个解,则实数a的取值范围( )
|
| A、[1,2] |
| B、(-∞,2) |
| C、[1,+∞) |
| D、(-∞,1) |
设P为曲线y2=
x上任一点,F1(-5,0),F2(5,0),则下列命题正确的是( )
| 3 |
| 4 |
| A、||PF1|-|PF2||≥8 |
| B、||PF1|-|PF2||≤8 |
| C、||PF1|-|PF2||>8 |
| D、||PF1|-|PF2||<8 |
函数y=
在区间[
,2]上的最小值为( )
| ex |
| x |
| 1 |
| 2 |
A、2
| ||
B、
| ||
C、
| ||
| D、e |
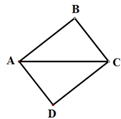 已知ABCD矩形中,AB=4,AD=3,在水平位置的平面α上画出矩形ABCD的直观图A′B′C′D′,并使对角线AC平行于y轴,则A′B′C′D′的面积为( )
已知ABCD矩形中,AB=4,AD=3,在水平位置的平面α上画出矩形ABCD的直观图A′B′C′D′,并使对角线AC平行于y轴,则A′B′C′D′的面积为( )