题目内容
如图所示,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,
AD=PD=2EA=2,F, G, H分别为BP, BE, PC的中点。
(1)求证:平面FGH⊥平面AEB;
(2)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
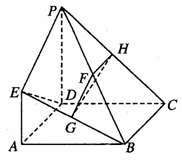
证明:(1)因为EA⊥平面ABCD,所以EA⊥CB.
又因为CB⊥AB,AB∩AE=A,所以CB⊥平面ABE.…3分
由已知F,H分别为线段PB,PC的中点,所以FH∥BC,则FH⊥平面ABE.……5分
而FH⊂平面FGH,所以平面FGH⊥平面ABE.
(2)在线段PC上存在一点M,使PB⊥平面EFM.证明如下:在直角三角形AEB中,因为AE=1,AB=2,所以BE=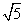 ,
,
在直角梯形EADP中,因为AE=1,AD=PD=2,所以PE=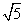 ,所以PE=BE.
,所以PE=BE.
又因为F为PB的中点,所以EF⊥PB.
要使PB⊥平面EFM,只需使PB⊥FM
因为PD⊥平面ABCD,所以PD⊥CB,又因为CB⊥CD,PD∩CD=D,
所以CB⊥平面PCD,而PC⊂平面PCD,所以CB⊥PC.
若PB⊥FM,则△PFM∽△PCB,可得 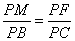 ,
,
由已知可求得PB= ,PF=
,PF=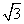 ,PC=
,PC=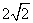 ,所以PM=
,所以PM=

练习册系列答案
相关题目
 ·
· =0,则
=0,则 = 。
= 。 是减函数的概率为 。
是减函数的概率为 。 :
: ,
, :
: ,则
,则 的导数为
的导数为 ,则数列
,则数列 的前
的前 项和是( )
项和是( ) B.
B. C.
C. D.
D.
 在R上可导,且
在R上可导,且 =
= ,则( )
,则( ) B.
B.  C.
C. D. 不能确定
D. 不能确定