题目内容
17．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（3，m），若向量$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为3，则实数m=（ ）| A． | 3 | B． | -3 | C． | $\sqrt{3}$ | D． | -3$\sqrt{3}$ |
分析 由投影的定义即可求出m．
解答 解：根据投影的定义：$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{3+\sqrt{3}m}{2}$=3，解得m=$\sqrt{3}$，
故选：C．
点评 考查投影的概念，向量夹角的余弦公式，向量数量积的坐标运算，以及根据向量坐标求向量长度．
练习册系列答案
相关题目
5．已知sinφ=$\frac{3}{5}$，且φ∈（$\frac{π}{2}$，π），函数f（x）=sin（ωx+φ）（ω＞0）的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$，则f（$\frac{π}{4}$）的值为（ ）
| A． | -$\frac{3}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
12．已知圆O：x2+y2=4上到直线l：x+y=a的距离等于1的点至少有2个，则a的取值范围为（ ）
| A． | （-3$\sqrt{2}$，3$\sqrt{2}$） | B． | （-∞，-3$\sqrt{2}$）∪（3$\sqrt{2}$，+∞） | C． | （-2$\sqrt{2}$，2$\sqrt{2}$） | D． | [-3$\sqrt{2}$，3$\sqrt{2}$] |
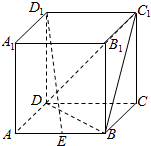如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E为棱AB的中点．