题目内容

7．已知复数（1+i）z=1-i（i是虚数单位），则z的共轭复数的虚部是（　　）
A．iB．1C．-iD．-1

分析 利用复数的运算法则、共轭复数与虚部的定义即可得出．

解答 解：（1+i）z=1-i（i是虚数单位），∴（1-i）（1+i）z=（1-i）（1-i），∴2z=-2i，化为z=-i
则z的共轭复数i的虚部是1．
故选：B．

点评 本题考查了复数的运算法则、共轭复数与虚部的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
17．某早餐店每天制作甲、乙两种口味的糕点共n（n∈N*）份，每份糕点的成本1元，售价2元，如果当天卖不完，剩下的糕点作废品处理，该早餐店发现这两种糕点每天都有剩余，为此整理了过往100天这两种糕点的日销量（单位：份），得到如下统计数据：
 甲口味糕点日销量 48 49 50 51
 天数 20 40 20 20
 乙口味糕点日销量 48 49 50 51
 天数 40 30 20 10
以这100天记录的各销量的频率作为各销量的概率，假设这两种糕点的日销量相互独立．
（1）记该店这两种糕点每日的总销量为X份，求X的分布列；
（2）早餐店为了减少浪费，提升利润，决定调整每天制作糕点的份数．
①若产生浪费的概率不超过0.6，求n的最大值；
②以销售这两种糕点的日总利润的期望值为决策依据，在每天所制糕点能全部卖完与n=98之中选其一，应选哪个？
18．设函数f（x）=|x-a|+|2x+2|-5（a∈R）．
（Ⅰ）试比较f（-1）与f（a）的大小；
（Ⅱ）当a≥-1时，若函数f（x）的图象和x轴围成一个三角形，则实数a的取值范围．
15．若实数x，y满足约束条件$\left\{\begin{array}{l}x-y-1≤0\\ x+3≥0\\ y-2≤0\end{array}\right.$，则z=2x-y的最大值为（　　）
A．-8B．-6C．-2D．4
2．已知圆C：（x-1）2+y2=$\frac{1}{4}$，一动圆与直线x=-$\frac{1}{2}$相切且与圆C外切．
（Ⅰ）求动圆圆心P的轨迹T的方程；
（Ⅱ）若经过定点Q（6，0）的直线l与曲线T相交于A、B两点，M是线段AB的中点，过M作x轴的平行线与曲线T相交于点N，试问是否存在直线l，使得NA⊥NB，若存在，求出直线l的方程，若不存在，说明理由．
12．过点P（-1，1）作圆C：（x-t）2+（y-t）2=1（t∈R）的切线，切点分别为A，B，则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为0．
19．已知等比数列{an}的各项均为正数，且2a1，$\frac{{a}_{3}}{2}$，a2成等差数列，则$\frac{{a}_{2017}+{a}_{2016}}{{a}_{2015}+{a}_{2014}}$=（　　）
A．2B．3C．4D．9
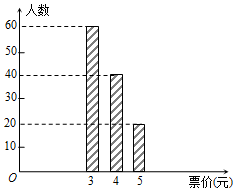16．已知某地铁1号线上，任意一站到M站的票价不超过5元，现从那些只乘坐1号线地铁，且在M站出站的乘客中随机选出120人，他们乘坐地铁的票价统计如图所示．
（I）如果从那些只乘坐1号线地铁，且在M站出站的乘客中任选1人，试估计此人乘坐地铁的票价小于5元的概率；
（II）已知选出的120人中有6名学生，且这6人乘坐地铁的票价情形恰好与按票价从这120中分层抽样所选的结果相同，现从这6人中随机选出2人，求这2人的票价和恰好为8元的概率．
17．为选拔选手参加“中国汉字听写大全”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．

（Ⅰ）求样本容量n和频率分布直方图中的x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“中国汉字听写大会”，每次抽取1人，求在第1次抽取的成绩低于90分的前提下，第2次抽取的成绩仍低于90分的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网