题目内容
在区间[0,π]上,关于α的方程5sinα+4=|5cosα+2|解的个数为 .
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:利用换元法,令5cosα=x,5sinα=y,则原方程化为y+4=|x+2|,x,y满足x2+y2=25,于是,方程5sinα+4=|5cosα+2|解的个数问题转化为绝对值函数图象与半圆的交点个数问题.
解答:
解:令
,α∈[0,π],则x2+y2=25,y∈[0,5].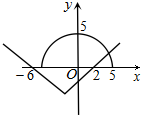
从而方程5sinα+4=|5cosα+2|化为y=|x+2|-4,
当x≥-2时,y=x-2;当x<-2时,y=-x-6,
由此,作出y=|x+2|-4的图象,
考察x2+y2=25的上半圆与函数y=|x+2|-4的图象,可知两图象有一个公共点,
故α的值唯一,即关于α的方程5sinα+4=|5cosα+2有1个解.
|

从而方程5sinα+4=|5cosα+2|化为y=|x+2|-4,
当x≥-2时,y=x-2;当x<-2时,y=-x-6,
由此,作出y=|x+2|-4的图象,
考察x2+y2=25的上半圆与函数y=|x+2|-4的图象,可知两图象有一个公共点,
故α的值唯一,即关于α的方程5sinα+4=|5cosα+2有1个解.
点评:1.本题若直接解三角方程,计算量较大,运用换元及数形结合思想,将三角方程转化为半圆与绝对值函数图象的交点问题,思路非常巧妙,大大简化了求解过程.
2.本题考查了圆的参数方程的应用,对于方程的解的个数问题,一般有以下两种方法:
(1)几何法:运用数形结合思想,转化为两图象的交点个数问题;
(2)代数法:联立方程组,消去适当的元,得到一个一元二次方程,根据判别式△判断.
2.本题考查了圆的参数方程的应用,对于方程的解的个数问题,一般有以下两种方法:
(1)几何法:运用数形结合思想,转化为两图象的交点个数问题;
(2)代数法:联立方程组,消去适当的元,得到一个一元二次方程,根据判别式△判断.

练习册系列答案
相关题目
从学号为0~50的燕中高二某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A、1,2,3,4,5 |
| B、5,16,27,38,49 |
| C、2,4,6,8,10 |
| D、4,13,22,31,40 |