题目内容
有下列四个命题：
①“若x+y=0，则x，y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
③“若q≤1，则方程x2+2x+q=0有实根”的逆否命题；
④“等边三角形的三个内角相等”的否命题．
⑤“若a＞b，则ac2＞bc2”的逆命题
其中真命题的序号是 ．
①“若x+y=0，则x，y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
③“若q≤1，则方程x2+2x+q=0有实根”的逆否命题；
④“等边三角形的三个内角相等”的否命题．
⑤“若a＞b，则ac2＞bc2”的逆命题
其中真命题的序号是
考点：命题的真假判断与应用
专题：综合题
分析：①写出逆命题并判定真假性；
②写出否命题并判定真假性；
③由互为逆否命题的两个命题真假性相同，判定原命题的真假性即可；
④写出否命题，再判定真假性；
⑤写出逆命题，在判定真假性．
②写出否命题并判定真假性；
③由互为逆否命题的两个命题真假性相同，判定原命题的真假性即可；
④写出否命题，再判定真假性；
⑤写出逆命题，在判定真假性．
解答：
解：对于①，“若x+y=0，则x，y互为相反数”的逆命题是“若x，y互为相反数，则x+y=0，”它是真命题；
②“全等三角形的面积相等”的否命题是“如果两个三角形不是全等三角形，那么这两个三角形的面积不相等”，它是假命题；
③∵q≤1时，△=4-4q≥0，∴方程x2+2x+q=0有实根，∴它的逆否命题是真命题；
④“等边三角形的三个内角相等”的否命题是“如果一个三角形不是等边三角形，那么它的三个内角不都相等”，它是真命题；
⑤“若a＞b，则ac2＞bc2”的逆命题是“若ac2＞bc2，则a＞b”，它是真命题．
综上，以上真命题有①③④⑤．
故答案为：①③④⑤．
②“全等三角形的面积相等”的否命题是“如果两个三角形不是全等三角形，那么这两个三角形的面积不相等”，它是假命题；
③∵q≤1时，△=4-4q≥0，∴方程x2+2x+q=0有实根，∴它的逆否命题是真命题；
④“等边三角形的三个内角相等”的否命题是“如果一个三角形不是等边三角形，那么它的三个内角不都相等”，它是真命题；
⑤“若a＞b，则ac2＞bc2”的逆命题是“若ac2＞bc2，则a＞b”，它是真命题．
综上，以上真命题有①③④⑤．
故答案为：①③④⑤．
点评：本题通过命题的真假性判定，考查了四种命题之间的关系，方程根的判定问题，不等式的性质与应用等知识，是综合性题目．
练习册系列答案
相关题目
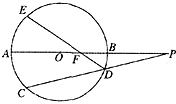已知⊙O的半径R=2，P为直径AB延长线上一点，PB=3，割线PDC交⊙O于D，C两点，E为⊙O上一点，且