题目内容
已知
=(-1,0,2),
=(2,0,t)且
∥
,则t的值为 .
| a |
| b |
| a |
| b |
考点:向量的数量积判断向量的共线与垂直
专题:空间位置关系与距离
分析:利用空间向量平行的性质求解.
解答:
解:∵
=(-1,0,2),
=(2,0,t),且
∥
,
∴2×2=-1×t,
解得t=-4.
∴t的值为-4.
故答案为:-4.
| a |
| b |
| a |
| b |
∴2×2=-1×t,
解得t=-4.
∴t的值为-4.
故答案为:-4.
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意空间向量平行的性质的合理运用.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
曲线y=2x3-6x上切线平行于x轴的点的坐标是( )
| A、(-1,4) |
| B、(1,-4) |
| C、(-1,-4)或(1,4) |
| D、(-1,4)或(1,-4) |
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2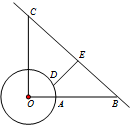 为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为
为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为