题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c.若sinA:sinB:sinC=6:5:4,则最大角为 .
考点:余弦定理,正弦定理
专题:解三角形
分析:已知比例式利用正弦定理化简,求出三边之比,利用余弦定理求出cosA的值,即可确定出最大角A的度数.
解答:
解:利用正弦定理化简sinA:sinB:sinC=6:5:4,得a:b:c=6:5:4,
∴cosA=
=
=
,
则A=arccos
.
故答案为:arccos
∴cosA=
| b2+c2-a2 |
| 2bc |
| 25+16-36 |
| 40 |
| 1 |
| 8 |
则A=arccos
| 1 |
| 8 |
故答案为:arccos
| 1 |
| 8 |
点评:此题考查了正弦、余弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式(x+1)(3-x)<0的解集是( )
| A、(-1,3) |
| B、(-∞,-1)∪(3,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |
已知
=1-yi,其中x,y是实数,i是虚数单位,则复数x+yi的共轭复数对应的点位于为( )
| x |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |





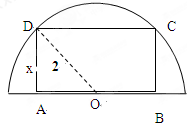 如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,
如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,