题目内容
已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )


A、f(x)=2sin(
| ||||
B、f(x)=
| ||||
C、f(x)=2cos(
| ||||
D、f(x)=2sin(4x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数的图象
专题:三角函数的图像与性质
分析:设设f(x)=Asin(ωx+φ)(A>0,ω>0),由图易知T=4π,从而可求得ω,排除B、D;再利用f(0)=1对A、C进行分析即可得到答案.
解答:
解:设f(x)=Asin(ωx+φ)(A>0,ω>0),
由图知,
=
•
=π,
∴ω=
,可排除B、D;
对于A,f(0)=2sin(-
)=-1,与题意f(0)=1不符,可排除A;
对于C,f(x)=2cos(
-
)=2sin[
(
-
)]=2sin(
+
),满足f(0)=1,当x0=
时,f(x0)=y0=2,满足题意;
故选:C.
由图知,
| T |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
∴ω=
| 1 |
| 2 |
对于A,f(0)=2sin(-
| π |
| 6 |
对于C,f(x)=2cos(
| x |
| 2 |
| π |
| 3 |
| π |
| 2 |
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
故选:C.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查排除法的应用,突出考查分析问题、解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| ∫ | 2π 0 |
| A、0 | B、2 | C、-2 | D、4 |
在算法中,流程图有三大基本结构,以下哪个不在其中( )
| A、顺序结构 | B、选择结构 |
| C、判断结构 | D、循环结构 |
设全集U=R,A={x|-3<x<0},B={x|x<-1},则图中阴影部分表示的集合为( )
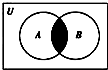

| A、(-3,-1) |
| B、(-1,0) |
| C、[-1,0) |
| D、(-∞,-1) |
下列函数为偶函数的是( )
| A、y=|x-1| | ||
| B、y=x3 | ||
C、y=
| ||
D、y=ln
|
点P(tan2012°,cos2012°)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知全集U=R,集合A={x|y=
},B={x|y=loga(x+2)},则集合(∁UA)∩B=( )
| 1 | ||
|
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-∞,-2) |
| D、(-1,+∞) |
 函数f(x)(x∈R)的图象如图所示,则函数g(x)=logaf(x)(0<a<1)的减区间是( )
函数f(x)(x∈R)的图象如图所示,则函数g(x)=logaf(x)(0<a<1)的减区间是( )A、(0,
| ||||
B、(-∞,0)∪[
| ||||
C、[
| ||||
D、[
|