题目内容
在下列命题中,假命题是( )
| A、存在x∈R,lgx=0 |
| B、存在x∈R,tanx=0 |
| C、任意x∈R,2x>0 |
| D、任意x∈R,x3>0 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.取x=1,使得lgx=0;
B.取x=0,则tan0=0;
C.?x∈R,2x>0;
D.取x=-1,(-1)3<0,即可判断出.
B.取x=0,则tan0=0;
C.?x∈R,2x>0;
D.取x=-1,(-1)3<0,即可判断出.
解答:
解:对于A.取x=1,使得lgx=0,正确;
对于B.取x=0,则tan0=0,正确;
对于C.?x∈R,2x>0,正确;
对于D.取x=-1,(-1)3<0,因此不正确.
故选:D.
对于B.取x=0,则tan0=0,正确;
对于C.?x∈R,2x>0,正确;
对于D.取x=-1,(-1)3<0,因此不正确.
故选:D.
点评:本题考查了简易逻辑的判定、举反例否定一个命题的方法,考查了推理能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
| A、①② | B、①③ | C、②③ | D、③④ |
若
,
均为单位向量,且
•
=0,(
-
)•(
-
)≤0,则|2
-
|的最大值为( )
|
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列运算正确的是( )
| A、(ax2-bx+c)′=a(x2)′+b(-x)′ |
| B、(cosx•sinx)′=(sinx)′•cosx+(cosx)′•cosx |
| C、(sinx-2x2)′=(sinx)′-(2)′(x2)′ |
| D、[(3+x2)(2-x3)]′=2x(2-x3)+3x2(3+x2) |
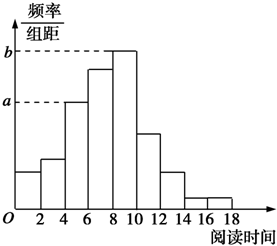 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图: 如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O,E是AB边的中点,EO的延长线交CD于F.
如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O,E是AB边的中点,EO的延长线交CD于F.