题目内容
(理科)下列命题中,正确的命题序号为 .
①方程组
的解集为{1,2},
②集合C={
∈z|x∈N*}={-6,-3,-2,-1,3,6}
③f(x)=
+
是函数
④f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a]则f(0)=1
⑤集合A={1,2,3,4},B={3,4,5,6}满足S⊆A且S∩B≠∅的集合S的个数为12个
⑥函数y=
在定义域内是减函数.
①方程组
|
②集合C={
| 6 |
| 3-x |
③f(x)=
| x-3 |
| 2-x |
④f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a]则f(0)=1
⑤集合A={1,2,3,4},B={3,4,5,6}满足S⊆A且S∩B≠∅的集合S的个数为12个
⑥函数y=
| 2 |
| x |
考点:命题的真假判断与应用
专题:计算题,函数的性质及应用,集合
分析:由集合的表示方法,解方程组,即可得到解集,即可判断①;运用列举法,结合自然数集和整数集的概念,即可判断②;求出定义域,即可判断③;运用偶函数的定义,即可得到a,b,进而得到f(x),f(0)=1,即可判断④;运用集合的包含关系,以及交集的定义,列举即可判断⑤;求出函数的单调区间,可举反例说明,即可判断⑥.
解答:
解:对于①,方程组
即为
,则解集为{(1,-2)},则①错;
对于②,由x∈N*,则x=1,2,4,5,6,9时,
=3,6,-6,-3,-2,-1.则②对;
对于③,由x-3≥0且2-x≥0,解得x∈∅,则f(x)不为函数.则③错;
对于④,f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a-1+2a=0,即有a=
,
又f(x)关于y轴对称,则b=0,f(x)=
x2+1,f(0)=1.则④对;
对于⑤,集合A={1,2,3,4},B={3,4,5,6}满足S⊆A且S∩B≠∅,
则S={3},{1,3},{2,3},{1,2,3},{4},{1,4},{2,4},{1,2,4},
{3,4},{1,3,4},{2,3,4},{1,2,3,4}.共12个,则⑤对;
对于⑥,函数y=
在(-∞,0),(0,+∞)均为减函数,比如f(-1)<f(1),则⑥错.
故答案为:②④⑤.
|
|
对于②,由x∈N*,则x=1,2,4,5,6,9时,
| 6 |
| 3-x |
对于③,由x-3≥0且2-x≥0,解得x∈∅,则f(x)不为函数.则③错;
对于④,f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a-1+2a=0,即有a=
| 1 |
| 3 |
又f(x)关于y轴对称,则b=0,f(x)=
| 1 |
| 3 |
对于⑤,集合A={1,2,3,4},B={3,4,5,6}满足S⊆A且S∩B≠∅,
则S={3},{1,3},{2,3},{1,2,3},{4},{1,4},{2,4},{1,2,4},
{3,4},{1,3,4},{2,3,4},{1,2,3,4}.共12个,则⑤对;
对于⑥,函数y=
| 2 |
| x |
故答案为:②④⑤.
点评:本题考查集合的表示方法、集合与集合间的关系,考查函数的定义、单调性和奇偶性的判断和运用,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
已知函数f(x)=sin(2x+
)(x∈R)的最小正周期为π,为了得到函数g(x)=sin2x的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知直线kx-y=k-1与直线ky-x=2k,若0<k<
,则它们的交点在( )
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
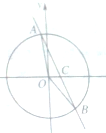 如图所示,在平面坐标系中,直线y=-2x+b(0<b<1)与单位圆x2+y2=1相交于A,B(A在第二象限)两个不同的点,且∠AOB=α,∠BOC=β,则cos(α-2β)的值是( )
如图所示,在平面坐标系中,直线y=-2x+b(0<b<1)与单位圆x2+y2=1相交于A,B(A在第二象限)两个不同的点,且∠AOB=α,∠BOC=β,则cos(α-2β)的值是( )